题目内容
在Rt△ABC中,∠C=90°,∠A=60°,从顶点C出发,在∠ACB内等可能地引射线CD交线段AB于点D,则S△ACD≤
S△ABC的概率是( )
| 1 |
| 2 |
分析:取AB中点D0,得△ACD0的面积等于△ABC的面积的一半,易得△ACD0是等边三角形.当经过C点的射线CD位于∠ACD0内部时,满足S△ACD≤
S△ABC,因此用∠ACD0的度数除以∠ABC的度数,即得本题的概率.
| 1 |
| 2 |
解答:解:取AB中点D0,得△ACD0的面积等于△ABC的面积的一半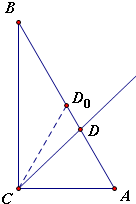
∵Rt△ABC中,∠C=90°,∠A=60°,
∴CD0=AD0=AC=
AB,可得∠ACD0=60°
当经过C点的射线CD位于∠ACD0内部时,S△ACD≤S△ACD0
即满足S△ACD≤
S△ABC,
∴所求概率为P=
=
=
故选:C

∵Rt△ABC中,∠C=90°,∠A=60°,
∴CD0=AD0=AC=
| 1 |
| 2 |
当经过C点的射线CD位于∠ACD0内部时,S△ACD≤S△ACD0
即满足S△ACD≤
| 1 |
| 2 |
∴所求概率为P=
| ∠ACD0 |
| ∠ABC |
| 60° |
| 90° |
| 2 |
| 3 |
故选:C
点评:本题给出含有60°的直角三角形,求射线截三角形所得面积小于直角三角形面积一半的概率,着重考查了几何概型及其计算方法的知识,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC=
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC= (几何证明选讲选做题)
(几何证明选讲选做题)