题目内容
 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.(1)求证:BC∥平面A1DE;
(2)求证:BC⊥平面A1DC;
(3)当D点在何处时,A1B的长度最小,并求出最小值.
分析:根据线线平行⇒线面平行证明(1);根据线面垂直?线线垂直可证(2);
设AD=x或设DC=x,利用垂直关系判定△,△A1CB,△A1DC的形状,构造以A1B为变量,x为自变量的函数,求函数的最小值即可.
设AD=x或设DC=x,利用垂直关系判定△,△A1CB,△A1DC的形状,构造以A1B为变量,x为自变量的函数,求函数的最小值即可.
解答: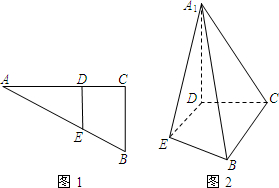 解:(本小题共14分)
解:(本小题共14分)
(1)证明:∵DE∥BC,DE?面A1DE,BC?面A1DE
∴BC∥面A1DE…(4分)
(2)证明:在△ABC中,∠C=90°,DE∥BC,
∴AD⊥DE∴A1D⊥DE.
又A1D⊥CD,CD∩DE=D,∴A1D⊥面BCDE.
由BC?面BCDE,
∴A1D⊥BC.BC⊥CD,A1D∩CD=D,
∴BC⊥面A1DC.…(9分)
(3)设DC=x则A1D=6-x由(Ⅱ)知,△A1CB,△A1DC均为直角三角形.
A1B=
=
,即A1B=
=
=
…(12分)
当x=3时,A1B的最小值是3
.
即当D为AC中点时,A1B的长度最小,最小值为3
.…(14分)
 解:(本小题共14分)
解:(本小题共14分) (1)证明:∵DE∥BC,DE?面A1DE,BC?面A1DE
∴BC∥面A1DE…(4分)
(2)证明:在△ABC中,∠C=90°,DE∥BC,
∴AD⊥DE∴A1D⊥DE.
又A1D⊥CD,CD∩DE=D,∴A1D⊥面BCDE.
由BC?面BCDE,
∴A1D⊥BC.BC⊥CD,A1D∩CD=D,
∴BC⊥面A1DC.…(9分)
(3)设DC=x则A1D=6-x由(Ⅱ)知,△A1CB,△A1DC均为直角三角形.
A1B=
| A1C2+BC2 |
| A1D2+DC2+BC2 |
| x2+32+(6-x)2 |
| 2x2-12x+45 |
| 2(x-3)2+27 |
当x=3时,A1B的最小值是3
| 3 |
即当D为AC中点时,A1B的长度最小,最小值为3
| 3 |
点评:本题考查线面平行、垂直的判定与空间中点、点距离的最值问题.设出变量,构造函数利用求函数最值的方法求解,是此类题的常用方法.

练习册系列答案
相关题目
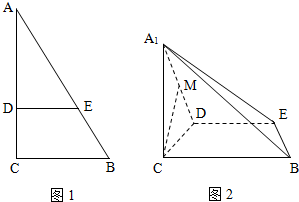 (2012•北京)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(2012•北京)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2. (2012•北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
(2012•北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2. 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2. (2013•宜宾二模)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.
(2013•宜宾二模)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.