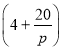题目内容
【题目】如图,在三棱锥D﹣ABC中,O为线段AC上一点,平面ADC⊥平面ABC,且△ADO,△ABO为等腰直角三角形,斜边AO=4![]() .
.
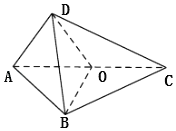
(Ⅰ)求证:AC⊥BD;
(Ⅱ)将△BDO绕DO旋转一周,求所得旋转体的体积.
【答案】(Ⅰ)证明见解析 (Ⅱ)16π
【解析】
(Ⅰ)推导出![]() ,取AO中点E,连结DEBE,,则
,取AO中点E,连结DEBE,,则![]() ,从而 AC⊥平面BDE ,即可得证(Ⅱ)由题意将△BDO绕DO旋转一周,所得到的旋转体是以2
,从而 AC⊥平面BDE ,即可得证(Ⅱ)由题意将△BDO绕DO旋转一周,所得到的旋转体是以2![]() 为底面半径,2为高的两公共底面的锥,即可求出旋转体的体积.
为底面半径,2为高的两公共底面的锥,即可求出旋转体的体积.
(Ⅰ)证明:∵△ADO,△ABO为等腰直角三角形,斜边AO=4![]() .
.
∴DO⊥AD,BO⊥AB,AD=DO=AB=BO=4,
取AO中点E,连结DEBE,如图,
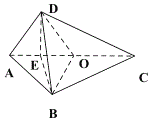
则DE⊥AC,BE⊥AC,且DE∩BE=E,
∴AC⊥平面BDE,
又BD平面BDE,∴AC⊥BD.
(Ⅱ)由(Ⅰ)知DE⊥AC,
∵平面ADC⊥平面ABC,且平面ADC∩平面ABC=AC,
∴DE⊥平面ABC,∴△BDE是直角三角形,
∵△ADO,△ABO是直角三角形,斜边AO=4![]() ,
,
∴BO=DO=4,DE=2![]() ,BE=2
,BE=2![]() ,
,
∴将△BDO绕DO旋转一周,所得到的旋转体是以2![]() 为底面半径,2为高的两公共底面的锥,
为底面半径,2为高的两公共底面的锥,
∴将△BDO绕DO旋转一周所得旋转体的体积为:![]() 16π.
16π.

练习册系列答案
相关题目