题目内容
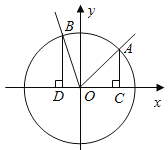
【题目】设![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两个不相等的实数根,那么过两点
的两个不相等的实数根,那么过两点![]() 、
、![]() 的直线与圆
的直线与圆![]() 的位置关系是( )
的位置关系是( )
A.相离B.相切C.相交D.随![]() 的变化而变化
的变化而变化
【答案】C
【解析】
根据方程有根可得![]() ,由根与系数的关系算出
,由根与系数的关系算出![]() ,
,![]() ,再利用直线的斜率公式算出AB的斜率
,再利用直线的斜率公式算出AB的斜率![]() ,利用中点坐标公式算出AB的中点,得出直线AB的方程,最后利用点到直线的距离公式,算出已知圆的圆心C到直线AB的距离小于圆C的半径,可得直线与圆的位置关系是相交.
,利用中点坐标公式算出AB的中点,得出直线AB的方程,最后利用点到直线的距离公式,算出已知圆的圆心C到直线AB的距离小于圆C的半径,可得直线与圆的位置关系是相交.
∵![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两个不相等的实数根,
的两个不相等的实数根,
∴![]() ,即
,即![]() ,且
,且![]() ,
,![]() ,
,
可得![]() ,
,
因此直线AB的斜率![]() ,AB的中点为
,AB的中点为![]() ,
,
即![]() ,
,
∴直线AB的方程为![]() ,化简得
,化简得![]() ,
,
又∵圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径
,半径![]() ,
,
∴圆心C到直线AB的距离为![]() ,
,
∵![]() ,可得
,可得![]() ,
,
∴圆心C到直线AB的距离小于圆C的半径,可得直线与圆的位置关系是相交.
故选:C.

练习册系列答案
相关题目