题目内容
已知数列 的前
的前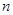 项和是
项和是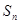 ,满足
,满足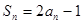 .
.
(Ⅰ)求数列 的通项
的通项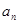 及前
及前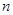 项和
项和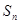 ;
;
(Ⅱ)若数列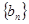 满足
满足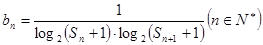 ,求数列
,求数列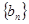 的前
的前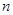 项和
项和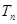 ;
;
(Ⅲ)若对任意的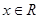 ,恒有
,恒有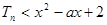 成立,求实数
成立,求实数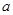 的取值范围
的取值范围
 的前
的前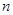 项和是
项和是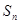 ,满足
,满足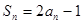 .
.(Ⅰ)求数列
 的通项
的通项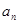 及前
及前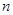 项和
项和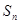 ;
;(Ⅱ)若数列
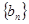 满足
满足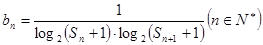 ,求数列
,求数列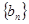 的前
的前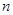 项和
项和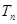 ;
;(Ⅲ)若对任意的
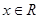 ,恒有
,恒有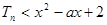 成立,求实数
成立,求实数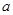 的取值范围
的取值范围 (1)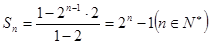 . (2)
. (2)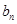
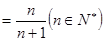
(3)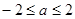
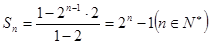 . (2)
. (2)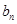
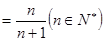
(3)
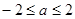
(I)先求出a1,然后构造由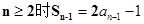 ,再与
,再与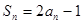 作差可得
作差可得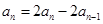 ,进而确定
,进而确定 是等比数列.问题得解.
是等比数列.问题得解.
(II)在(I)问的基础上,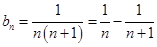 采用裂项求和方法求和.
采用裂项求和方法求和.
(III) 由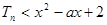 恒成立 , 即
恒成立 , 即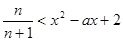 恒成立
恒成立
即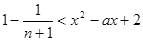 恒成立 ,必须且只须满足
恒成立 ,必须且只须满足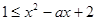 恒成立,然后转化为关于
恒成立,然后转化为关于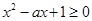 对于一切实数x恒成立即可.
对于一切实数x恒成立即可.
解:(I)由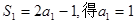 ,…………1分
,…………1分
由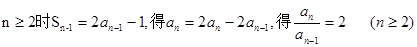 ---------2分
---------2分
∴数列 是等比数列
是等比数列 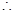 数列
数列 的公比q="2"
的公比q="2"
所以,数列 的通项公式为
的通项公式为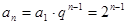
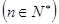 …………3分
…………3分
前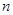 项和公式为
项和公式为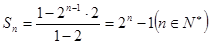 . ………………………4分
. ………………………4分
(II)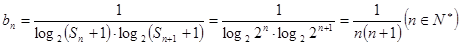
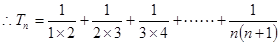 ……………………………6分
……………………………6分
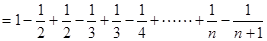 ………………………7分
………………………7分
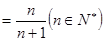 …………………………………………8分
…………………………………………8分
(Ⅲ)由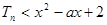 恒成立 即
恒成立 即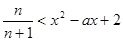 恒成立
恒成立
即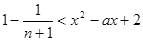 恒成立 ……………………………………9分
恒成立 ……………………………………9分
必须且只须满足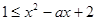 恒成立 ………………………………10分
恒成立 ………………………………10分
即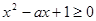 在R上恒成立
在R上恒成立 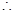
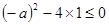 ,………………11分
,………………11分
解得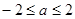 .
.
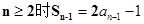 ,再与
,再与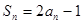 作差可得
作差可得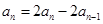 ,进而确定
,进而确定 是等比数列.问题得解.
是等比数列.问题得解.(II)在(I)问的基础上,
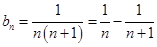 采用裂项求和方法求和.
采用裂项求和方法求和.(III) 由
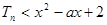 恒成立 , 即
恒成立 , 即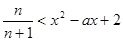 恒成立
恒成立即
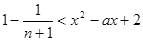 恒成立 ,必须且只须满足
恒成立 ,必须且只须满足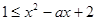 恒成立,然后转化为关于
恒成立,然后转化为关于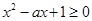 对于一切实数x恒成立即可.
对于一切实数x恒成立即可.解:(I)由
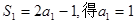 ,…………1分
,…………1分由
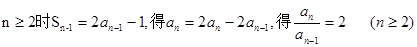 ---------2分
---------2分∴数列
 是等比数列
是等比数列 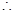 数列
数列 的公比q="2"
的公比q="2" 所以,数列
 的通项公式为
的通项公式为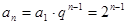
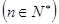 …………3分
…………3分前
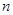 项和公式为
项和公式为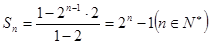 . ………………………4分
. ………………………4分(II)
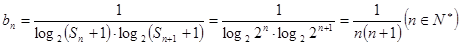
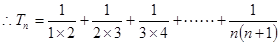 ……………………………6分
……………………………6分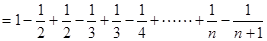 ………………………7分
………………………7分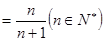 …………………………………………8分
…………………………………………8分(Ⅲ)由
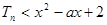 恒成立 即
恒成立 即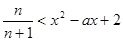 恒成立
恒成立即
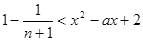 恒成立 ……………………………………9分
恒成立 ……………………………………9分必须且只须满足
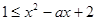 恒成立 ………………………………10分
恒成立 ………………………………10分即
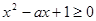 在R上恒成立
在R上恒成立 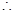
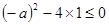 ,………………11分
,………………11分解得
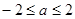 .
. 
练习册系列答案
相关题目
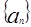 满足
满足 ,则称数列
,则称数列 的首项
的首项 ,前
,前 项和
项和 .(Ⅰ)求数列
.(Ⅰ)求数列 ,
, ,
, 为数列
为数列 的前
的前 .
.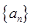 中,
中,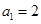 ,
,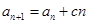 (
(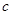 是常数,
是常数,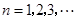 ),且
),且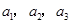 成公比不为
成公比不为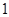 的等比数列。
的等比数列。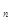 },求
},求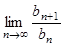 的值。
的值。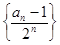 为等差数列;
为等差数列;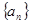 ,若
,若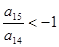 ,且它的前
,且它的前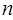 项和
项和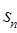 有最大值,那么当
有最大值,那么当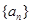 的前n项和为
的前n项和为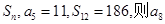 =( )
=( ) 中,已知前15项的和
中,已知前15项的和 ,则
,则 等于( )
等于( )

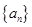 中,公差
中,公差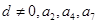 成等比数列,则
成等比数列,则 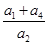 = ;
= ;