题目内容
已知数列{an}中,a1=5且an=2an-1+2n-1(n≥2且n∈N*).
(Ⅰ)证明:数列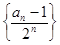 为等差数列;
为等差数列;
(Ⅱ)求数列{ an-1}的前n项和Sn
(Ⅰ)证明:数列
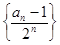 为等差数列;
为等差数列;(Ⅱ)求数列{ an-1}的前n项和Sn
(1)数列 为首项是2公差是1的等差数列.
为首项是2公差是1的等差数列.
(2)Sn=n·2n+1
 为首项是2公差是1的等差数列.
为首项是2公差是1的等差数列.(2)Sn=n·2n+1
(1)根据等差数列的定义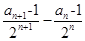 是定值即可.
是定值即可.
(2)在第(I)问的基本上求出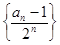 的通项公式,进而求出{ an-1}的通项公式,然后根据数列求和的方法求值即可。
的通项公式,进而求出{ an-1}的通项公式,然后根据数列求和的方法求值即可。
解:(Ⅰ)设bn=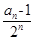 , b1=
, b1=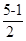 =2 ……………………………………………1分
=2 ……………………………………………1分
bn+1- bn=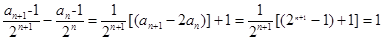 …4分
…4分
所以数列 为首项是2公差是1的等差数列. …………………………5分
为首项是2公差是1的等差数列. …………………………5分
(Ⅱ)由(Ⅰ)知,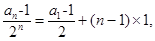
∴an-1=(n+1)·2n …………………………7分
∵Sn=2·21+3·22+…+n·2n-1+(n+1)·2n ①
∴2Sn=2·22+3·23+…+ n·2n+(n+1)·2n+1 ②……………………9分
①—②,得 - Sn=4+(22+23+…+2n)-(n+1)·2n+1
∴Sn=-4-4(2n+1-1)+(n+1)·2n+1
∴Sn=n·2n+1
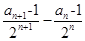 是定值即可.
是定值即可.(2)在第(I)问的基本上求出
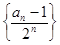 的通项公式,进而求出{ an-1}的通项公式,然后根据数列求和的方法求值即可。
的通项公式,进而求出{ an-1}的通项公式,然后根据数列求和的方法求值即可。解:(Ⅰ)设bn=
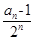 , b1=
, b1=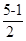 =2 ……………………………………………1分
=2 ……………………………………………1分bn+1- bn=
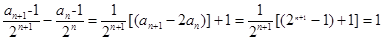 …4分
…4分所以数列
 为首项是2公差是1的等差数列. …………………………5分
为首项是2公差是1的等差数列. …………………………5分(Ⅱ)由(Ⅰ)知,
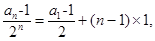
∴an-1=(n+1)·2n …………………………7分
∵Sn=2·21+3·22+…+n·2n-1+(n+1)·2n ①
∴2Sn=2·22+3·23+…+ n·2n+(n+1)·2n+1 ②……………………9分
①—②,得 - Sn=4+(22+23+…+2n)-(n+1)·2n+1
∴Sn=-4-4(2n+1-1)+(n+1)·2n+1
∴Sn=n·2n+1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
,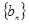 满足:
满足: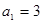 ,当
,当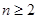 时,
时,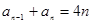 ;对于任意的正整数
;对于任意的正整数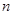 ,
,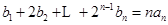 .设
.设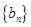 的前
的前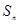 .
.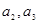 ,并求数列
,并求数列
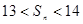 的
的 的前
的前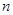 项和是
项和是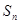 ,满足
,满足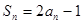 .
.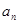 及前
及前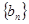 满足
满足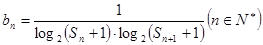 ,求数列
,求数列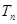 ;
;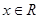 ,恒有
,恒有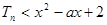 成立,求实数
成立,求实数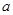 的取值范围
的取值范围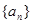 是等差数列,其中
是等差数列,其中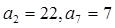 (1).求
(1).求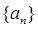 的通项;
的通项; 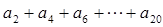 值;(3)设数列
值;(3)设数列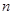 项和为
项和为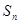 ,求
,求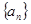 (
(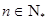 )中,已知
)中,已知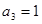 ,
,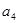 是
是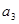 和
和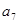 的等比中项.
的等比中项.
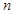 项和为
项和为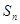 ,求使
,求使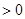 时
时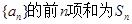 ,首项为1的等比数列
,首项为1的等比数列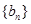 的公比为
的公比为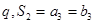 ,且
,且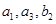 成等比数列。
成等比数列。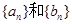 的通项公式;
的通项公式;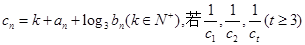 成等差数列,求k和t的值。
成等差数列,求k和t的值。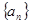 中,
中, 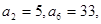 则
则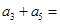 ______________
______________ 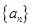 中,前15项的和
中,前15项的和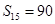 ,
, 为( )
为( )