题目内容
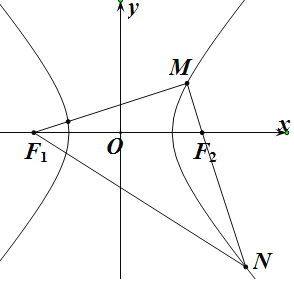
【题目】已知![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,M为双曲线右支上一点且满足
的左、右焦点,M为双曲线右支上一点且满足![]() ,若直线
,若直线![]() 与双曲线的另一个交点为N,则
与双曲线的另一个交点为N,则![]() 的面积为__________.
的面积为__________.
【答案】24
【解析】
设|![]() |=m,|
|=m,|![]() |=n,根据双曲线的定义知
|=n,根据双曲线的定义知![]() ,可求出m=6,n=2,再设|
,可求出m=6,n=2,再设|![]() |=t,则|
|=t,则|![]() |=4+t根据勾股定理求出t=6即可求出三角形的面积
|=4+t根据勾股定理求出t=6即可求出三角形的面积
设|![]() |=m,|
|=m,|![]() |=n,
|=n,
∵![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,
的左、右焦点,
∴m﹣n=2a=4,|![]() |=2c=2
|=2c=2![]()
∵![]() ,
,
∴![]() ,
,
∴m2+n2=4c2=40,
∴(m﹣n)2=m2+n2﹣2mn,
即2mn=40﹣16=24,
∴mn=12,
解得m=6,n=2,
设|![]() |=t,则|
|=t,则|![]() |=2a+t=4+t
|=2a+t=4+t
在Rt![]() 中可得(4+t)2=(t+2)2+62,
中可得(4+t)2=(t+2)2+62,
解得t=6,
∴|MN|=6+2=8,
∴![]() 的面积S
的面积S![]() |MN||M
|MN||M![]() |
|![]() 8×6=24
8×6=24
故答案为24.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: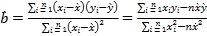 ,
, ![]() ./span>
./span>