题目内容
已知函数f(x)＝x2＋xsin x＋cos x.
(1)若曲线y＝f(x)在点(a，f(a))处与直线y＝b相切，求a与b的值；
(2)若曲线y＝f(x)与直线y＝b有两个不同交点，求b的取值范围．
(1)若曲线y＝f(x)在点(a，f(a))处与直线y＝b相切，求a与b的值；
(2)若曲线y＝f(x)与直线y＝b有两个不同交点，求b的取值范围．
(1) a＝0，b＝1.(2) b>1
(1)由f(x)＝x2＋xsin x＋cos x，
得f′(x)＝x(2＋cos x)，
∵y＝f(x)在点(a，f(a))处与直线y＝b相切．
∴f′(a)＝a(2＋cos a)＝0且b＝f(a)，
则a＝0，b＝f(0)＝1.
(2)令f′(x)＝0，得x＝0.
∴当x>0时，f′(x)>0，f(x)在(0，＋∞)递增．
当x<0时，f′(x)<0，f(x)在(－∞，0)上递减．
∴f(x)的最小值为f(0)＝1.
由于函数f(x)在区间(－∞，0)和(0，＋∞)上均单调，
所以当b>1时曲线y＝f(x)与直线y＝b有且仅有两个不同交点．
得f′(x)＝x(2＋cos x)，
∵y＝f(x)在点(a，f(a))处与直线y＝b相切．
∴f′(a)＝a(2＋cos a)＝0且b＝f(a)，
则a＝0，b＝f(0)＝1.
(2)令f′(x)＝0，得x＝0.
∴当x>0时，f′(x)>0，f(x)在(0，＋∞)递增．
当x<0时，f′(x)<0，f(x)在(－∞，0)上递减．
∴f(x)的最小值为f(0)＝1.
由于函数f(x)在区间(－∞，0)和(0，＋∞)上均单调，
所以当b>1时曲线y＝f(x)与直线y＝b有且仅有两个不同交点．
练习册系列答案
相关题目
.其中
.
的值;
,若
,求
，
．
，求函数
的单调区间；
恒成立，求实数
的取值范围；
，若对任意的两个实数
满足
，总存在
，使得
成立，证明：
．
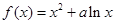的图像在点
处的切线斜率为10. 
的值;
根的个数,并证明你的结论;
,使得曲线
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
的最小值；
，
．
时，
的图象与
的图象有唯一的公共点；
时，
的取值范围．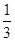
x3＋ax2＋(a2－1)x＋1(a∈R)的导函数y＝f′(x)图象，则f(－1)等于________．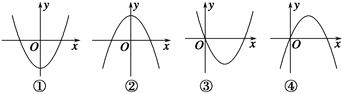
x3＋
x2－ax－a，x∈R，其中a＞0.
的值域为 ．