题目内容
已知函数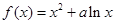 的图像在点
的图像在点 处的切线斜率为10.
处的切线斜率为10.
(1)求实数 的值;
的值;
(2)判断方程 根的个数,并证明你的结论;
根的个数,并证明你的结论;
(21)探究: 是否存在这样的点 ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
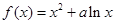 的图像在点
的图像在点 处的切线斜率为10.
处的切线斜率为10. (1)求实数
 的值;
的值;(2)判断方程
 根的个数,并证明你的结论;
根的个数,并证明你的结论;(21)探究: 是否存在这样的点
 ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.(1)8;(2)一个,证明参考解析;(21)

试题分析:(1)曲线上切线的斜率是通过导数的几何意义,求曲线的导数再将该点的横坐标代入即可求得该点的斜率,从而可解得
 的值.
的值.(2)判断方程的根的情况,一般是通过构造新的函数从而证明函数的与x轴的交点的个数得到对应方程的根的个数.
(21)因为是否存在这样的点
 ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧.是通过说明过该点的切线方程与曲线方程联立后,构建一个新的函数,要说明该点不是新函数的极值点即可.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧.是通过说明过该点的切线方程与曲线方程联立后,构建一个新的函数,要说明该点不是新函数的极值点即可.试题解析:(1)因为
 .图像在点
.图像在点 处的切线斜率为10,
处的切线斜率为10, .解得
.解得 .
.(2)方程
 只有一个实根.证明如下:由(1)可知
只有一个实根.证明如下:由(1)可知 ,令
,令 ,因为
,因为 ,
, ,所以在
,所以在 内至少有一个实根.又因为
内至少有一个实根.又因为 .所以
.所以 在
在 递增,所以函数
递增,所以函数 在
在 上有且只有一个零点,及方程
上有且只有一个零点,及方程 有且只有一个实根.
有且只有一个实根.(21)由
 ,
, ,可求得曲线
,可求得曲线 在点
在点 处的切线方程为
处的切线方程为 .即
.即 .记
.记
 ,
, .若存在这样的点
.若存在这样的点 ,使得曲线
,使得曲线 在该点附近的左右两部分分别位于曲线在该点处切线的两侧,则问题等价于
在该点附近的左右两部分分别位于曲线在该点处切线的两侧,则问题等价于 不是极值点,由二次函数的性质可知,当且仅当
不是极值点,由二次函数的性质可知,当且仅当 时,
时, 不是极值点,即
不是极值点,即 .所以
.所以 在
在 上递增.又
上递增.又 ,所以当
,所以当 时,
时, ,当
,当 时,
时, ,即存在唯一点
,即存在唯一点 .使得曲线在点A附近的左右两部分分别位于曲线在该点处切线的两侧.
.使得曲线在点A附近的左右两部分分别位于曲线在该点处切线的两侧.
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
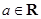 ,函数
,函数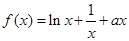 .
.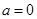 时,求
时,求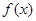 的最小值;
的最小值;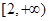 上是单调函数,求
上是单调函数,求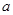 的取值范围.
的取值范围.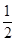 x2(a>0),若对定义域内的任意x,f′(x)≥2恒成立,则a的取值范围是________.
x2(a>0),若对定义域内的任意x,f′(x)≥2恒成立,则a的取值范围是________.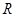 上的可导函数
上的可导函数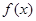 ,恒有
,恒有 ,(其中
,(其中 表示函数
表示函数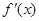 在
在 的值),则
的值),则 ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值. +ln x,若函数f(x)在[1,+∞)上为增函数,则正实数a的取值范围是______.
+ln x,若函数f(x)在[1,+∞)上为增函数,则正实数a的取值范围是______. ,则
,则 ( )
( )


