题目内容
【题目】下列四个命题:
①函数![]() 的最大值为1;
的最大值为1;
②“若![]() ,则
,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
③若![]() 为锐角三角形,则有
为锐角三角形,则有![]() ;
;
④“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件.
内单调递增”的充分必要条件.
其中所有正确命题的序号为____________.
【答案】③④
【解析】
利用二倍角公式化简函数,可得![]() ,根据正弦型函数值域可知①错误;确定原命题的逆命题后,通过
,根据正弦型函数值域可知①错误;确定原命题的逆命题后,通过![]() 可知逆命题为假,②错误;利用诱导公式和角的范围可证得结论,③正确;分类讨论去掉函数中的绝对值符号,根据二次函数的性质可确定函数的单调性,从而得到满足题意的范围,进而说明充要条件成立,④正确.
可知逆命题为假,②错误;利用诱导公式和角的范围可证得结论,③正确;分类讨论去掉函数中的绝对值符号,根据二次函数的性质可确定函数的单调性,从而得到满足题意的范围,进而说明充要条件成立,④正确.
①![]()
![]() ,①错误
,①错误
②“若![]() ,则
,则![]() ”的逆命题为:“若
”的逆命题为:“若![]() ,则
,则![]() ”
”
若![]() ,可知
,可知![]() ,则其逆命题为假命题,②错误
,则其逆命题为假命题,②错误
③![]() 为锐角三角形
为锐角三角形 ![]() ,
,![]() ,
,![]()
![]() 且
且![]()
![]()
同理可得:![]() ,
,![]()
![]() ,③正确
,③正确
④令![]() ,解得:
,解得:![]() ,
,![]()
当![]() 时,
时,![]() 对
对![]() 恒成立
恒成立 ![]()
![]() 对称轴为
对称轴为![]()
![]() 在
在![]() 上单调递增,充分条件成立
上单调递增,充分条件成立
当![]() 时,
时,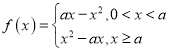 ,此时
,此时![]() 在
在![]() 上单调递减,不满足题意
上单调递减,不满足题意
![]() “
“![]() ”是“
”是“![]() 在区间
在区间![]() 内单调递增”的充分必要条件,④正确
内单调递增”的充分必要条件,④正确
本题正确结果:③④

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目