题目内容
【题目】某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
A小区 | 低碳族 | 非低碳族 |
比例 |
|
|
B小区 | 低碳族 | 非低碳族 |
比例 |
|
|
C小区 | 低碳族 | 非低碳族 |
比例 |
|
|
(1)从A,B,C三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:
(1)利用题意结合概率公式可得恰好有2人是低碳族的概率是![]() ;
;
(2)由题意可得所给的分布列为超几何分布,且X的取值为0,1,2,3,据此求解分布列即可.
试题解析:
(1)记这3人中恰好有2人是低碳族为事件A,P(A)=![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() =
=![]() .
.
(2)在B小区中随机选择20户中,“非低碳族”有4户,
P(X=k)=![]() (k=0,1,2,3),
(k=0,1,2,3),
所以X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|

练习册系列答案
相关题目
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了![]() 名女性或
名女性或![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
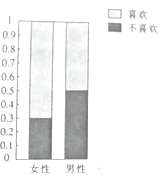
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
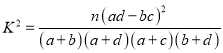 ,其中
,其中![]()