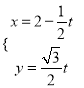题目内容
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ)当![]() 时,若曲线
时,若曲线![]() 上总存在相异两点
上总存在相异两点![]() ,使曲线
,使曲线![]() 在
在![]() 两点处的切线互相平行,试求
两点处的切线互相平行,试求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(1)求导数,对![]() 分类讨论,利用导数的正负,即可得到
分类讨论,利用导数的正负,即可得到![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)利用过![]() 两点处的切线互相平行,建立方程,结合基本不等式,再求最值,即可求解
两点处的切线互相平行,建立方程,结合基本不等式,再求最值,即可求解![]() 的取值范围。
的取值范围。
试题解析:(Ⅰ)由已知得, ![]() 的定义域为
的定义域为![]() ,且
,且
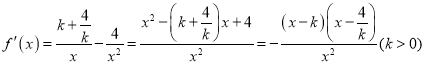 ,
,
①当![]() 时,
时, ![]() ,且
,且![]() ,
,
所以![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .
.
所以,函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
②当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 内恒成立,
内恒成立,
所以![]() 在
在![]() 上是减函数;
上是减函数;
③当![]() 时,
时, ![]() ,
,
所以![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]()
所以函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(Ⅱ)由题意,可得![]() ,
, ![]() 且
且![]()
即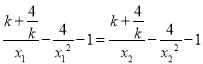 ,化简得,
,化简得, ![]()
由![]() ,得
,得![]()
即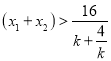 对
对![]() 恒成立,
恒成立,
令![]() ,则
,则![]() 对
对![]() 恒成立
恒成立
∴![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,所以
,所以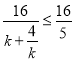 ,
,
所以![]() ,
,
故![]() 取值范围为
取值范围为![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目