题目内容
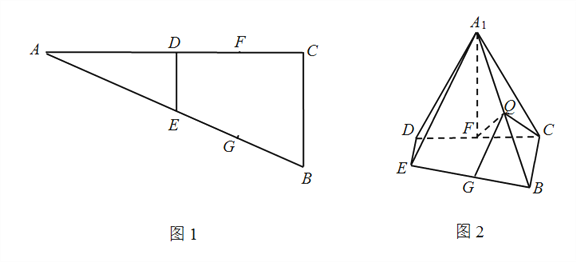
【题目】如图1,在![]() △
△![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为边
分别为边![]() 的中点,点
的中点,点![]() 分别为线段
分别为线段![]() 的中点.将△
的中点.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() .点
.点![]() 为线段
为线段![]() 上的一点,如图2.
上的一点,如图2.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长,若不存在,请说明理由;
的长,若不存在,请说明理由;
(Ⅲ)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)见解析(2)在线段![]() 上存在中点
上存在中点![]() ,使
,使![]() 平面
平面![]() .
.
且![]() (3)
(3)![]()
【解析】试题分析:(1)先根据等腰三角形性质得![]() .再由折叠中不变的垂直关系得
.再由折叠中不变的垂直关系得![]() ,根据线面垂直判定定理得
,根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]()
![]() .最后再根据线面垂直判定定理得
.最后再根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .(2)利用空间向量研究线面平行关系,即通过平面法向量与直线方向向量垂直进行研究,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据平面法向量与直线方向向量数量积为零列式求解参数.(3)利用空间向量求线面角,仍是先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据线面角与向量夹角之间互余关系列式求线面角大小.
.(2)利用空间向量研究线面平行关系,即通过平面法向量与直线方向向量垂直进行研究,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据平面法向量与直线方向向量数量积为零列式求解参数.(3)利用空间向量求线面角,仍是先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据线面角与向量夹角之间互余关系列式求线面角大小.
试题解析:解:(Ⅰ)
因为![]() ,
,
所以△![]() 为等边三角形.
为等边三角形.
又因为点![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() .
.
由题可知![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
(Ⅱ)由(Ⅰ)知![]() 平面
平面![]() ,
, ![]() ,如图
,如图
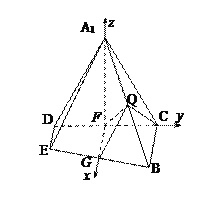
建立空间直角坐标系,则![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,
所以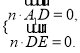 即
即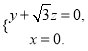
令![]() ,所以
,所以![]() ,所以
,所以![]()
假设在线段![]() 上存在点
上存在点![]() ,使img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/14/e30bb3b0/SYS201712291439006281273551_DA/SYS201712291439006281273551_DA.053.png" width="39" height="21" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />平面
,使img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/14/e30bb3b0/SYS201712291439006281273551_DA/SYS201712291439006281273551_DA.053.png" width="39" height="21" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />平面![]() .
.
设![]() ,
, ![]() .
.
又![]() ,所以
,所以![]() .
.
所以![]() .则
.则![]() .
.
所以![]() .
.
解得, ![]() .
.
则在线段![]() 上存在中点
上存在中点![]() ,使
,使![]() 平面
平面![]() .
.
且![]()
(Ⅲ)因为![]() ,又
,又![]() ,所以
,所以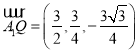 .
.
所以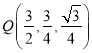 .又因为
.又因为![]() ,
,
所以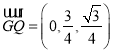 .
.
因为![]() 设直线
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则
直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案