题目内容
已知函数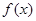 是定义在
是定义在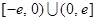 上的奇函数,当
上的奇函数,当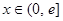 时,有
时,有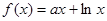 (其中
(其中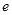 为自然对数的底,
为自然对数的底,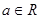 ).
).
(1)求函数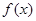 的解析式;
的解析式;
(2)设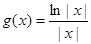 ,
,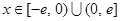 ,求证:当
,求证:当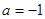 时,
时,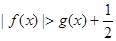 ;
;
(3)试问:是否存在实数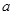 ,使得当
,使得当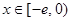 时,
时,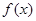 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数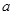 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
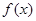 是定义在
是定义在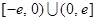 上的奇函数,当
上的奇函数,当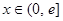 时,有
时,有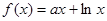 (其中
(其中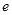 为自然对数的底,
为自然对数的底,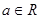 ).
).(1)求函数
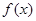 的解析式;
的解析式;(2)设
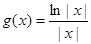 ,
,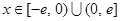 ,求证:当
,求证:当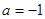 时,
时,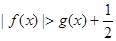 ;
;(3)试问:是否存在实数
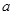 ,使得当
,使得当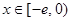 时,
时,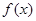 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数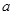 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.(1)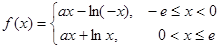
(2)构造函数利用函数的最小值大于另一个函数的最大值来证明成立。
(3)当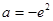 时,函数
时,函数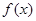 在区间
在区间 上的最小值是3
上的最小值是3
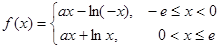
(2)构造函数利用函数的最小值大于另一个函数的最大值来证明成立。
(3)当
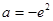 时,函数
时,函数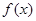 在区间
在区间 上的最小值是3
上的最小值是3试题分析:解:(1)当
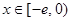 时,
时,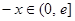 ,
,则
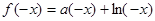 ,
,又
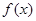 是奇函数,
是奇函数,所以
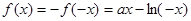 ,
,因此,
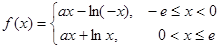 ; 4分
; 4分(2)证明:令
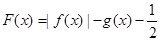 ,
,当
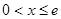 时,注意到
时,注意到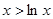 ,所以
,所以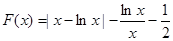
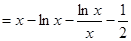 5分
5分① 当
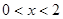 时,注意到
时,注意到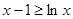 ,有
,有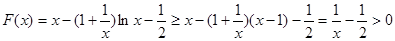 ; 6分
; 6分② 当
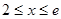 时,
时,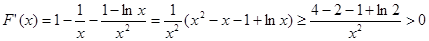 , 7分
, 7分故函数
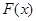 在
在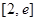 上是增函数,从而有
上是增函数,从而有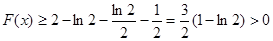 ,
,所以当
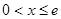 时,有
时,有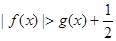 , 8分
, 8分又因为
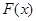 是偶函数,故当
是偶函数,故当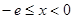 时,同样有
时,同样有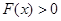 ,即
,即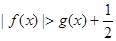 ,
,综上所述,当
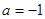 时,有
时,有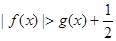 ; 9分
; 9分(2)证法二:当
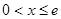 时,
时,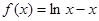 ,
,求导得
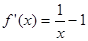 ,令
,令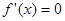 得
得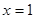 , 5分
, 5分于是可得当
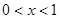 时,
时,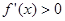 ;
;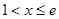 时,
时,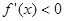 ,
,所以
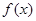 在
在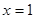 处取得最大值
处取得最大值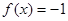 ,所以
,所以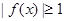 . 6分
. 6分又记
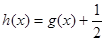 ,当
,当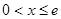 时,有
时,有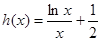 , 7分
, 7分求导得
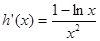 ,当
,当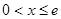 时,
时,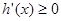 ,
,所以
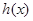 在
在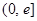 上单调递增,于是
上单调递增,于是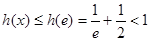 ,
,所以,在在
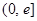 上总有
上总有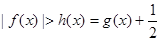 . 8分
. 8分注意到
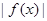 和
和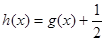 的偶函数性质,
的偶函数性质,所以当
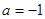 时,有
时,有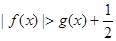 (
(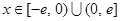 ); 9分
); 9分(3)当
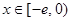 时,
时,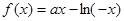 ,
,求导得
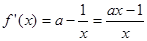 ,令
,令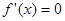 得
得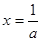 , 10分
, 10分① 当
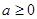 时,
时,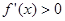 ,
,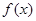 在区间
在区间 上是增函数,故此时函数
上是增函数,故此时函数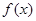 在区间
在区间 上的最小值为
上的最小值为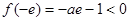 ,不满足要求; 11分
,不满足要求; 11分② 当
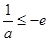 ,即
,即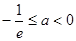 时,
时,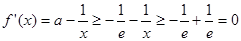 ,
,所以
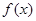 在区间
在区间 上是增函数,此时函数
上是增函数,此时函数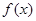 在区间
在区间 的最小值为
的最小值为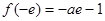 ,
,令
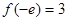 ,得
,得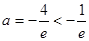 ,也不满足要求; 12分
,也不满足要求; 12分③ 当
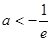 时,可得
时,可得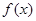 在区间
在区间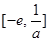 上是减函数,在区间
上是减函数,在区间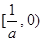 上是增函数,所以当
上是增函数,所以当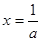 时,
时,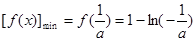 ,
,令
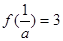 ,得
,得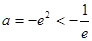 ,满足要求. 13分
,满足要求. 13分综上可得,当
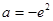 时,函数
时,函数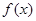 在区间
在区间 上的最小值是3. 14分
上的最小值是3. 14分点评:解决的关键是根据导数的符号于函数单调性的关系来判定单调性,进而得到最值,属于基础题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
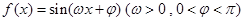 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表: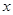
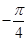

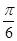
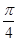
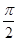
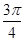
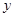
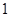
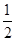
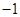
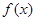 的解析式;
的解析式;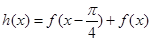 ,
,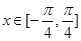 ,求
,求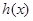 的最大值和最小值.
的最大值和最小值.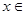 [0,
[0,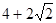 ]时y=f(x)= _____________
]时y=f(x)= _____________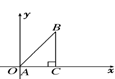
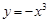
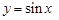
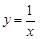
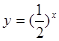
 的值域为[0,+
的值域为[0,+ ),则
),则 的最小
的最小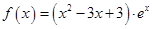 ,设
,设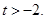
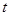 的取值范围,使得函数
的取值范围,使得函数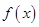 在
在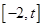 上为单调函数;
上为单调函数;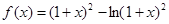 ,若关于
,若关于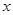 的方程
的方程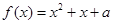 在
在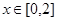 上恰好有两个相异实根,则实数
上恰好有两个相异实根,则实数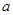 的取值范围为______________.
的取值范围为______________.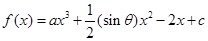 的图象过点
的图象过点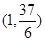 ,且在
,且在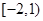 内单调递减,在
内单调递减,在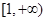 上单调递增。
上单调递增。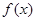 的解析式;
的解析式;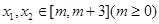 ,不等式
,不等式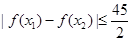 恒成立,试问这样的
恒成立,试问这样的 是否存在.若存在,请求出
是否存在.若存在,请求出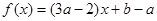 ,
, 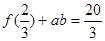 ,且
,且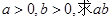 的取值范围
的取值范围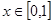 时,
时,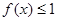 恒成立,且
恒成立,且 的取值范围
的取值范围