题目内容
已知函数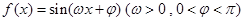 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表:
(I)求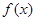 的解析式;
的解析式;
(II)设函数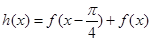 ,
,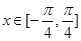 ,求
,求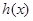 的最大值和最小值.
的最大值和最小值.
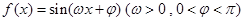 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表: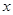 | 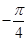 |  | 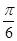 | 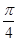 | 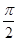 | 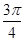 |
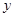 |  | 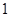 | 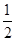 |  | 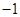 |  |
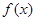 的解析式;
的解析式;(II)设函数
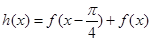 ,
,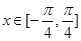 ,求
,求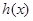 的最大值和最小值.
的最大值和最小值.(Ⅰ)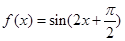 (或者
(或者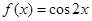 );(Ⅱ)
);(Ⅱ)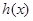 的最大值是2,最小值是
的最大值是2,最小值是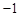 .
.
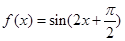 (或者
(或者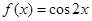 );(Ⅱ)
);(Ⅱ)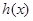 的最大值是2,最小值是
的最大值是2,最小值是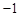 .
.试题分析:(Ⅰ)现根据表格数据的特点求最小正周期
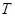 ,再利用公式
,再利用公式 求出
求出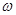 的值,然后再找图象的最高点或最低点或对称中心点确定
的值,然后再找图象的最高点或最低点或对称中心点确定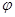 的值,这样便求出了函数
的值,这样便求出了函数 的解析式;(Ⅱ)先确定函数
的解析式;(Ⅱ)先确定函数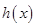 的解析式
的解析式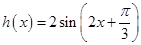 ,然后利用复合函数以及正弦函数的图象确定函数
,然后利用复合函数以及正弦函数的图象确定函数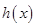 在区间
在区间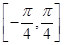 上的最小值与最大值,具体做法时,令
上的最小值与最大值,具体做法时,令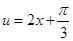 ,根据
,根据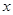 的范围确定
的范围确定 的取值范围
的取值范围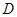 ,然后利用正弦函数
,然后利用正弦函数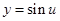 的图象确定
的图象确定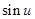 在区间
在区间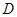 上的最值,进而求出函数数
上的最值,进而求出函数数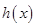 在区间
在区间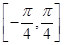 上的最小值与最大值.
上的最小值与最大值.试题解析:解:(Ⅰ)由表格给出的信息可以知道,函数
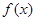 的周期为
的周期为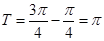 ,
,所以
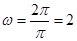 .由
.由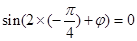 ,且
,且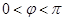 ,得
,得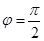 . 4分
. 4分所以函数解析式为
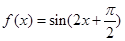 (或者
(或者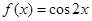 ). 6分
). 6分(Ⅱ)
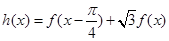
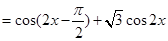
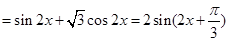 , 9分
, 9分又因为
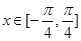 ,所以
,所以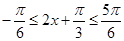 ,所以
,所以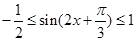 ,
,所以函数
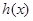 的最大值是2,最小值是
的最大值是2,最小值是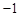 . 12分
. 12分
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 上的函数
上的函数 满足
满足 .若当
.若当 时。
时。 ,则当
,则当 时,
时,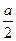 , 则a的值为 .
, 则a的值为 . (k≠0);⑤ y=sinx.
(k≠0);⑤ y=sinx.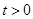 ,函数
,函数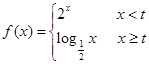 的值域为
的值域为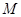 .若
.若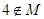 ,则
,则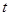 的取值范围是 .
的取值范围是 . 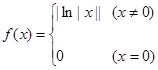 ,则方程
,则方程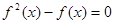 的不相等的实根个数为( )
的不相等的实根个数为( )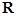 上的偶函数
上的偶函数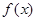 ,对任意实数
,对任意实数 都有
都有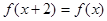 ,当
,当 时,
时,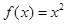 ,若在区间
,若在区间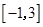 内,函数
内,函数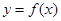 与函数
与函数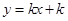 的图象恰有4个交点,则实数
的图象恰有4个交点,则实数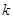 的取值范围是__________.
的取值范围是__________.  是定义在
是定义在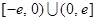 上的奇函数,当
上的奇函数,当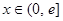 时,有
时,有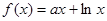 (其中
(其中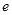 为自然对数的底,
为自然对数的底,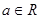 ).
).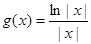 ,
,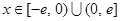 ,求证:当
,求证:当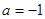 时,
时,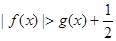 ;
; ,使得当
,使得当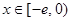 时,
时, ,则
,则 的图像大致为
的图像大致为