题目内容
设函数f(x)是定义在(-2,2)上的减函数,满足:f(-x)=-f(x),且f(m-1)+f(2m-1)>0,求实数m的取值范围.
不等式f(m-1)+f(2m-1)>0即f(m-1)>-f(2m-1),
∵f(-x)=-f(x),可得-f(2m-1)=f(-2m+1)
∴原不等式转化为f(m-1)>f(-2m+1)
又∵f(x)是定义在(-2,2)上的减函数,
∴-2<m-1<-2m+1<2,解之得-
<m<
即实数m的取值范围为(-
,
).
∵f(-x)=-f(x),可得-f(2m-1)=f(-2m+1)
∴原不等式转化为f(m-1)>f(-2m+1)
又∵f(x)是定义在(-2,2)上的减函数,
∴-2<m-1<-2m+1<2,解之得-
| 1 |
| 2 |
| 2 |
| 3 |
即实数m的取值范围为(-
| 1 |
| 2 |
| 2 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
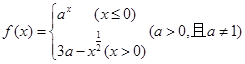 是
是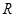 上的减函数,则
上的减函数,则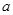 的取值范围是 .
的取值范围是 .