题目内容
已知函数f(x)为奇函数,x>0时为增函数且f(2)=0,则{x|f(x-2)>0}=( )
| A.{x|0<x<2或x>4} | B.{x|x<0或x>4} |
| C.{x|x<0或x>6} | D.{x|x<-2或x>2} |
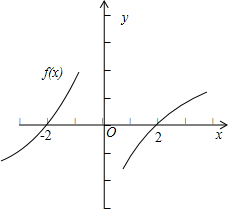
由于函数f(x)为奇函数,x>0时为增函数且f(2)=0,
可得函数在(-∞,0)上单调递增,且f(-2)=0,
故函数f(x)的单调性示意图如图所示:
由函数的图象可得-2<x-2<2,或-2x-2<0,
解得 0<x<2或x>4,
故选:A.
可得函数在(-∞,0)上单调递增,且f(-2)=0,
故函数f(x)的单调性示意图如图所示:
由函数的图象可得-2<x-2<2,或-2x-2<0,
解得 0<x<2或x>4,
故选:A.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



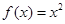 ,
, ,
,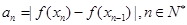 ,
,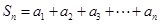 ,则
,则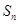 的最大值等于 .
的最大值等于 .