题目内容
已知数列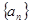 中,
中,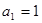 ,且
,且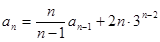 (
(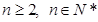 )。
)。
(I) 求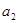 ,
,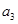 的值及数列
的值及数列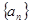 的通项公式;
的通项公式;
(II) (II)令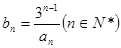 ,数列
,数列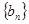 的前
的前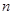 项和为
项和为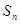 ,试比较
,试比较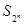 与
与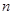 的大小;
的大小;
(III)令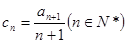 ,数列
,数列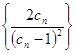 的前
的前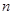 项和为
项和为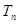 ,求证:对任意
,求证:对任意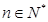 ,都有
,都有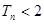 。
。
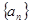 中,
中,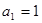 ,且
,且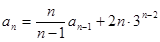 (
(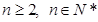 )。
)。(I) 求
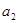 ,
,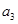 的值及数列
的值及数列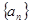 的通项公式;
的通项公式;(II) (II)令
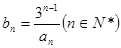 ,数列
,数列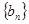 的前
的前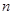 项和为
项和为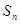 ,试比较
,试比较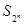 与
与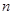 的大小;
的大小;(III)令
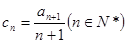 ,数列
,数列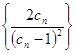 的前
的前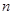 项和为
项和为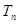 ,求证:对任意
,求证:对任意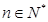 ,都有
,都有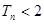 。
。(I)解:当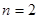 时,
时,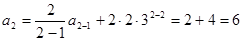 ,(1分)
,(1分)
当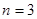 时,
时,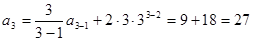 。(2分)
。(2分)
因为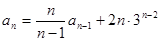 ,所以
,所以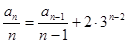 。(3分)
。(3分)
当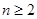 时,由累加法得
时,由累加法得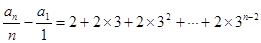 ,
,
因为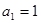 ,所以
,所以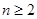 时,有
时,有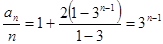 。
。
即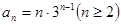 。
。
又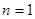 时,
时,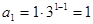 ,
,
故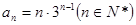 。(5分)
。(5分)
(II)解: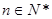 时,
时,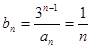 ,则
,则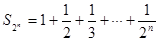 。
。
记函数 ,
,
所以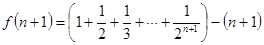 。
。
则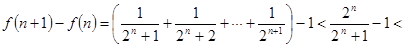 0。
0。
所以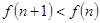 。(7分)
。(7分)
由于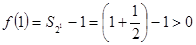 ,此时
,此时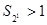 ;
;
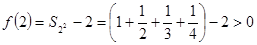 ,此时
,此时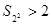 ;
;
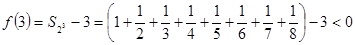 ,此时
,此时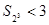 ;
;
由于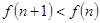 ,故
,故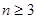 时,
时,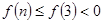 ,此时
,此时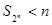 。
。
综上所述,当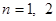 时,
时, ;当
;当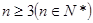 时,
时,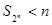 。(8分)
。(8分)
(III)证明:对于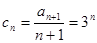 ,有
,有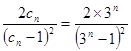 。
。
当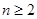 时,
时,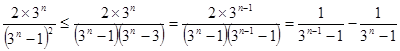 。
。
所以当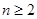 时,
时,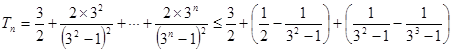
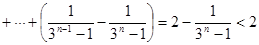 。
。
且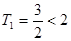 。
。
故对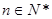 ,
,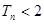 得证。(10分)
得证。(10分)
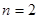 时,
时,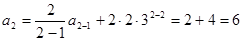 ,(1分)
,(1分)当
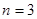 时,
时,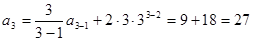 。(2分)
。(2分)因为
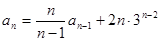 ,所以
,所以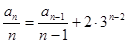 。(3分)
。(3分)当
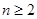 时,由累加法得
时,由累加法得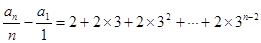 ,
,因为
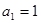 ,所以
,所以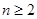 时,有
时,有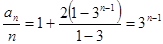 。
。即
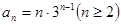 。
。又
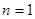 时,
时,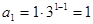 ,
,故
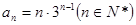 。(5分)
。(5分)(II)解:
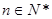 时,
时,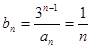 ,则
,则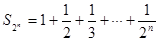 。
。记函数
 ,
,所以
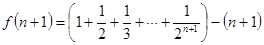 。
。则
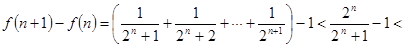 0。
0。所以
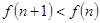 。(7分)
。(7分)由于
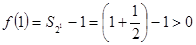 ,此时
,此时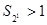 ;
;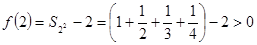 ,此时
,此时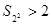 ;
;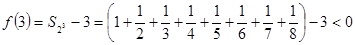 ,此时
,此时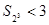 ;
;由于
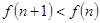 ,故
,故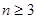 时,
时,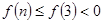 ,此时
,此时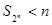 。
。综上所述,当
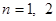 时,
时, ;当
;当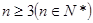 时,
时,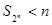 。(8分)
。(8分)(III)证明:对于
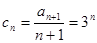 ,有
,有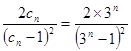 。
。当
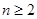 时,
时,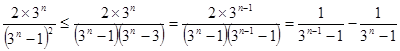 。
。所以当
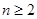 时,
时,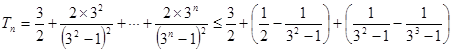
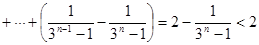 。
。且
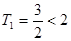 。
。故对
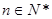 ,
,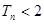 得证。(10分)
得证。(10分)本试题主要是考查了数列的通项公式与求和的综合运用,以及数列与不等式的关系的运用。
(1)利用已知的递推关系得到数列的前几项的值,并整体变形构造等差数列求解通项公式。
(2)利用第一问的结论,结合分组求和的思想和等比数列的求和得到结论。
(3))先分析通项公式的特点,然后裂项求和,证明不等是的成立问题。
(1)利用已知的递推关系得到数列的前几项的值,并整体变形构造等差数列求解通项公式。
(2)利用第一问的结论,结合分组求和的思想和等比数列的求和得到结论。
(3))先分析通项公式的特点,然后裂项求和,证明不等是的成立问题。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
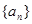 的前项
的前项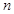 和为,已知
和为,已知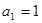 ,
,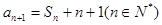 ,
,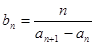 ,数列
,数列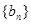 的前项和为
的前项和为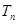 ,
,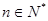 证明:
证明: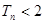 .
.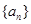 是一个等差数列,且
是一个等差数列,且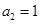 ,
,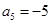 .(1)求
.(1)求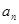 ;
;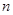 项和
项和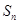 ;
;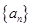 的前
的前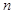 项和为
项和为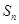 ,则下列说法错误的是 .
,则下列说法错误的是 .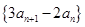 是等差数列;
是等差数列;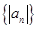 是等差数列;
是等差数列;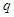 的等比数列,则
的等比数列,则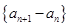 也是等比数列且公比为
也是等比数列且公比为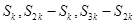
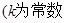
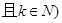 也是等比数列且公比为
也是等比数列且公比为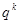 .
.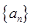 为等差数列,且
为等差数列,且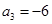 ,
,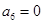 。
。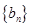 满足
满足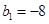 ,
,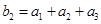 ,求数列
,求数列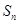 。
。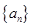 和
和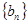 的前n项和分别为
的前n项和分别为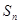 和
和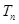 ,且
,且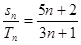 ,则
,则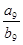 的值为()
的值为()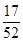
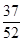
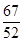

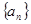 中,
中,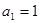 ,
,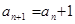 ,则
,则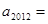
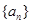 中,
中,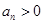 ,且
,且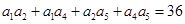 ,则
,则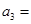 .
.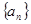 的前n项和
的前n项和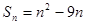 ,第k项满足
,第k项满足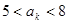 ,则k=_______
,则k=_______