题目内容
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪, 图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1).设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域;
(2).如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
(1)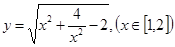 ;(2)如果DE是水管,DE的位置在AD=AE=
;(2)如果DE是水管,DE的位置在AD=AE= 处,如果DE是参观路线,则DE为AB中线或AC中线时,DE最长,证明过程详见解析.
处,如果DE是参观路线,则DE为AB中线或AC中线时,DE最长,证明过程详见解析.
解析试题分析:(1)在△ADE中,利用余弦定理可得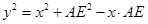 ,又根据面积公式可得
,又根据面积公式可得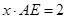 ,消去AE后即可得到y与x的函数关系式,又根据
,消去AE后即可得到y与x的函数关系式,又根据 可以得到x的取值范围;(2)如果DE是水管,则问题等价于当
可以得到x的取值范围;(2)如果DE是水管,则问题等价于当 时,求
时,求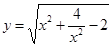 的最小值,利用基本不等式
的最小值,利用基本不等式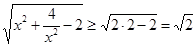 即可求得当
即可求得当 时,y有最小值为
时,y有最小值为 ,如果DE是参观路线,则问题等价于问题等价于当
,如果DE是参观路线,则问题等价于问题等价于当 时,求
时,求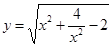 的最小值,根据函数
的最小值,根据函数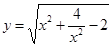 在[1,2]上的单调性,可得当x=1或2时,y有最小值
在[1,2]上的单调性,可得当x=1或2时,y有最小值 .
.
(1)在△ADE中,由余弦定理:

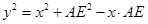 ①
①
又∵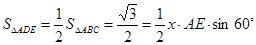

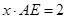 ②
②
②代入①得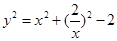 (y>0), ∴
(y>0), ∴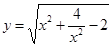 ,
,
由题意可知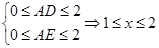 ,所以函数的定义域是
,所以函数的定义域是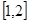 ,
, ;
;
(2)如果DE是水管
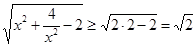 ,
,
当且仅当 ,即x=
,即x= 时“=”成立,故DE∥BC,且DE=
时“=”成立,故DE∥BC,且DE= .
.
如果DE是参观线路,记 ,可知函数在[1,
,可知函数在[1, ]上递减,在[
]上递减,在[ ,2]上递增,
,2]上递增,
故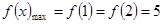 ∴y max=
∴y max= .即DE为AB中线或AC中线时,DE最长.
.即DE为AB中线或AC中线时,DE最长.
考点:1、平面向量的数量积;2、三角形面积计算.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 ,
, ,求三角形ABC的面积.
,求三角形ABC的面积. ,
,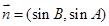 ,
, .
.
 //
// ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形; 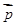 ,边长
,边长 ,角
,角
 ,求ΔABC的面积 .
,求ΔABC的面积 . 中,角A,B,C,的对边分别为
中,角A,B,C,的对边分别为 ,且
,且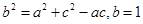
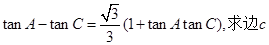 的值;
的值;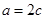 ,求
,求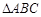 中,
中,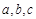 为角
为角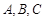 所对的边,且
所对的边,且 .
.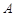 的值;
的值;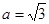 ,则求
,则求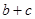 的取值范围.
的取值范围. .
. 中,已知
中,已知 ,
, 且
且 .
. 和
和 的值;
的值; ,求边
,求边 的长.
的长. +2cos2
+2cos2 ,x∈R.
,x∈R. ,求a的值.
,求a的值. 中,角
中,角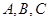 对的边分别为
对的边分别为 ,已知
,已知 .
. ,求
,求 的取值范围;
的取值范围; ,求
,求