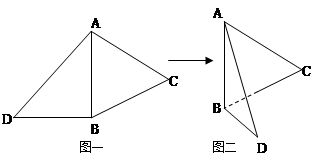题目内容
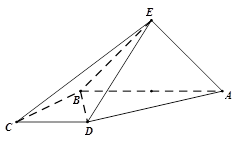
如图,将边长为2的正方形ABCD沿对角线BD折叠,使的平面ABD⊥平面CBD,AE⊥平面ABD,且AE=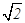 ,
,

(1) 求证:DE⊥AC
(2)求DE与平面BEC所成角的正弦值
(3)直线BE上是否存在一点M,使得CM//平面ADE,若存在,求M的位置,不存在,请说明理由。
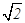 ,
,
(1) 求证:DE⊥AC
(2)求DE与平面BEC所成角的正弦值
(3)直线BE上是否存在一点M,使得CM//平面ADE,若存在,求M的位置,不存在,请说明理由。
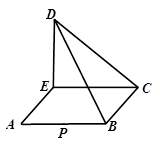
(1)以A为原点,以射线AB,AC,AE为坐标轴建立空间直角坐标系,
则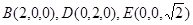 由C作平面ABD的垂线,垂足为F,则F为BC的中点,
由C作平面ABD的垂线,垂足为F,则F为BC的中点,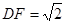 ,所以点C的坐标为
,所以点C的坐标为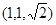 ,
,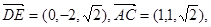
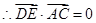
故:DE⊥AC(2)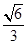 (3)存在M为BE的中点,使得CM//平面ADE
(3)存在M为BE的中点,使得CM//平面ADE
则
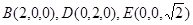 由C作平面ABD的垂线,垂足为F,则F为BC的中点,
由C作平面ABD的垂线,垂足为F,则F为BC的中点,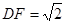 ,所以点C的坐标为
,所以点C的坐标为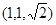 ,
,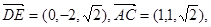
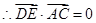
故:DE⊥AC(2)
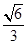 (3)存在M为BE的中点,使得CM//平面ADE
(3)存在M为BE的中点,使得CM//平面ADE试题分析:以A为原点,以射线AB,AC,AE为坐标轴建立空间直角坐标系,
则
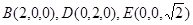
由C作平面ABD的垂线,垂足为F,则F为BC的中点,
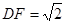 ,
,所以点C的坐标为
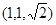 。
。(1)
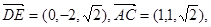
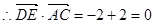 ,故:DE⊥AC。
,故:DE⊥AC。(2)

设平面BCE的法向量为
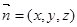 ,则
,则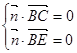 ,
,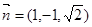
设线面角为
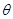 ,
,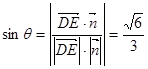
(3)设
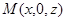 ,则
,则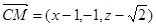 。若CM//平面ADE,则
。若CM//平面ADE,则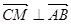 ,所以
,所以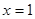 ,故存在M为BE的中点,使得CM//平面ADE。
,故存在M为BE的中点,使得CM//平面ADE。点评:采用空间向量的方法求解立体几何问题的步骤:建立空间直角坐标系,写出相关点及相关向量的坐标,将坐标代入证明或计算求解的对应公式求解,空间向量法要求学生数据处理时认真仔细

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 平面
平面 ,
, ,
, ,
, ,
, 分别为
分别为 的中点.
的中点.
 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. ,
, ∥
∥ ,
, .又
.又 ,
, ,直线AM与直线PC所成的角为
,直线AM与直线PC所成的角为 .
.
 ;
; 的余弦值.
的余弦值.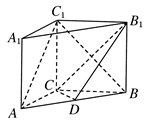
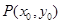
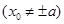 是双曲线
是双曲线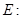
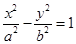
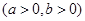 上一点,
上一点, 、
、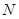 分别是双曲线
分别是双曲线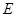 的左、右顶点,直线
的左、右顶点,直线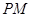 ,
,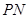 的斜率之积为
的斜率之积为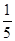 .
.
 ,
, 两点,
两点,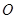 为坐标原点,
为坐标原点,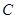 为双曲线上一点,满足
为双曲线上一点,满足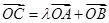 ,求
,求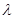 的值.
的值.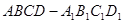 的底面边长是
的底面边长是 ,体积是
,体积是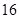 ,
,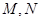 分别是棱
分别是棱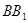 、
、 的中点.
的中点.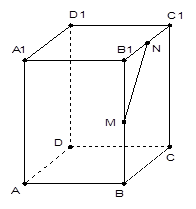
 与平面
与平面 所成的角(结果用反三角函数表示);
所成的角(结果用反三角函数表示);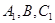 的平面与该正四棱柱所截得的多面体
的平面与该正四棱柱所截得的多面体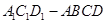 的体积.
的体积.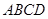 与
与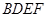 均为菱形,
均为菱形,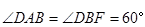 ,且
,且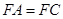 .
.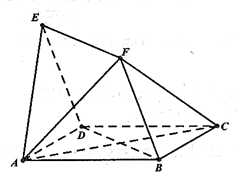
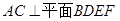 ;
;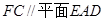 ;
;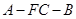 的余弦值.
的余弦值.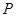 ,在直线DE上是否存在一点
,在直线DE上是否存在一点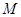 ,使得
,使得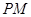 ∥面BCD?若存在,请指出点
∥面BCD?若存在,请指出点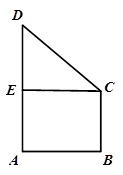
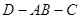 ,如图二,在二面角
,如图二,在二面角