题目内容
正方体 中,异面直线
中,异面直线 与
与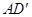 所成角度为 .
所成角度为 .
 中,异面直线
中,异面直线 与
与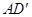 所成角度为 .
所成角度为 .
试题分析:如图,连结
 ,由正方体的性质可知
,由正方体的性质可知 ,所以
,所以 或其补角为异面直线
或其补角为异面直线 与
与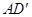 所成的角,而
所成的角,而 为正三角形,所以
为正三角形,所以 ,故异面直线
,故异面直线 与
与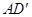 所成的角为
所成的角为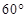 .
.

练习册系列答案
相关题目
题目内容
 中,异面直线
中,异面直线 与
与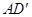 所成角度为 .
所成角度为 .
 ,由正方体的性质可知
,由正方体的性质可知 ,所以
,所以 或其补角为异面直线
或其补角为异面直线 与
与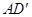 所成的角,而
所成的角,而 为正三角形,所以
为正三角形,所以 ,故异面直线
,故异面直线 与
与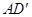 所成的角为
所成的角为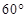 .
.
