题目内容
设函数 .
.
(I)若曲线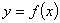 与曲线
与曲线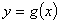 在它们的交点
在它们的交点 处具有公共切线,求
处具有公共切线,求 的值;
的值;
(II)当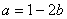 时,若函数
时,若函数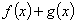 在区间
在区间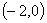 内恰有两个零点,求
内恰有两个零点,求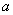 的取值范围;
的取值范围;
(III)当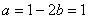 时,求函数
时,求函数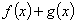 在区间
在区间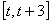 上的最大值
上的最大值
(I)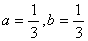 .(II)
.(II) 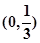 。(Ⅲ)
。(Ⅲ)
解析试题分析:(I)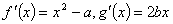 .
.
因为曲线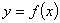 与曲线
与曲线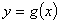 在它们的交点
在它们的交点 处具有公共切线,所以
处具有公共切线,所以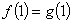 ,且
,且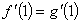 ,即
,即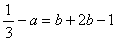 ,且
,且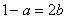 ,
,
解得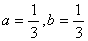 .
.
(II)记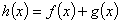 ,当
,当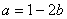 时,
时,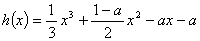 ,
,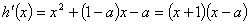 ,令
,令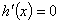 ,得
,得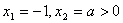 .
.
当 变化时,
变化时,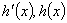 的变化情况如下表:
的变化情况如下表:
所以函数
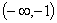
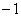
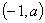
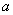

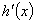
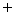
0 — 0 
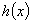
↗ 极大值 ↘ 极小值 ↗ 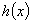 的单调递增区间为
的单调递增区间为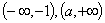 ;单调递减区间为
;单调递减区间为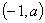 ,
, ①当
①当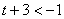 时,即
时,即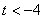 时,
时,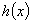 在区间
在区间

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
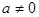 ,函数
,函数 .
. 有极大值32,求实数
有极大值32,求实数 的值;
的值; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 .
. 的极值;
的极值; 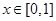 时,求
时,求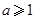 ,函数
,函数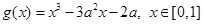 ,若对于任意
,若对于任意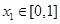 ,总存在
,总存在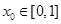 ,使得
,使得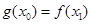 成立,求
成立,求 的取值范围.
的取值范围. 为常数,已知函数
为常数,已知函数 在区间
在区间 上是增函数,
上是增函数,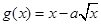 在区间
在区间 上是减函数.
上是减函数. 为函数
为函数 的图像上任意一点,求点
的图像上任意一点,求点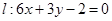 的距离的最小值;
的距离的最小值;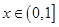 且
且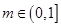 ,
, 恒成立,求实数
恒成立,求实数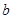 的取值范围.
的取值范围.
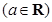 .
.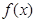 在定义域内的极值点的个数;
在定义域内的极值点的个数;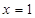 处取得极值,对
处取得极值,对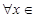
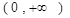 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.  在(-∞,+∞)上是增函数.
在(-∞,+∞)上是增函数.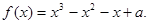
 的极值.
的极值.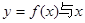 轴仅有一个交点.
轴仅有一个交点. 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.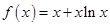 .
. 的图像在点
的图像在点 处的切线方程;
处的切线方程;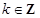 ,且
,且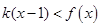 对任意
对任意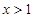 恒成立,求
恒成立,求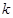 的最大值;
的最大值;