题目内容
用三段论证明函数 在(-∞,+∞)上是增函数.
在(-∞,+∞)上是增函数.
根据大前提导数大于零的区间即为单调增区间,那么求解导数得到增区间的证明。
解析试题分析:证明: . 当
. 当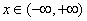 时,有
时,有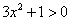 恒成立,
恒成立,
即在(-∞,+∞)上 恒成立.所以
恒成立.所以 在(-∞,+∞)上是增函数.
在(-∞,+∞)上是增函数.
考点:函数单调性
点评:解决的关键是利用导数的符号来判定函数的单调性,进而得到证明。

练习册系列答案
相关题目
题目内容
用三段论证明函数 在(-∞,+∞)上是增函数.
在(-∞,+∞)上是增函数.
根据大前提导数大于零的区间即为单调增区间,那么求解导数得到增区间的证明。
解析试题分析:证明: . 当
. 当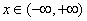 时,有
时,有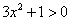 恒成立,
恒成立,
即在(-∞,+∞)上 恒成立.所以
恒成立.所以 在(-∞,+∞)上是增函数.
在(-∞,+∞)上是增函数.
考点:函数单调性
点评:解决的关键是利用导数的符号来判定函数的单调性,进而得到证明。
