Question

【题目】已知函数（）.

（1）若，求曲线在处的切线方程；

（2）若对任意， 恒成立，求实数的取值范围.

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）先根据导数几何意义得切线斜率为，再根据点斜式写切线方程（2）先将不等式恒成立转化为函数最值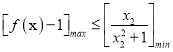： ,再利用导数求函数最小值为；根据导函数零点， ，分类讨论，确定导函数符号，进而确定单调性，最后由单调性确定最值取法，解对应不等式可得实数的取值范围.

试题解析：（1）依题意， ， ，故，

又，故所求切线方程为，即；

（2）令，故函数的定义域为， ．

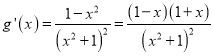当变化时， ， 的变化情况如下表：

	单调减	单调增	单调减

因为， ，所以时，函数的最小值为；

因为． 因为，令得， ， ．

（ⅰ）当，即时，在上，所以函数在上单调递增，所以函数．由得， ，所以．

（ⅱ）当，即时, 在上，在上，

所以函数在上单调递增，在上单调递减，所以，由得， ，所以．

综上所述， 的取值范围是.