题目内容
已知等比数列{an}满足a1=1,0<q<
,且对任意正整数k,ak-(ak+1+ak+2)仍是该数列中的某一项,则公比q的取值集合为______.
| 1 |
| 2 |
等比数列{an}的通项公式为an=qn-1,
ak-(ak+1+ak+2)qk•(
-1-q),
要使仍是该数列中的一项,则
-1-q=qn,
∵0<q<
,则
-1-q>
,
即q0=1或qn<
,
∴
-1-q=1,
即q2+2q-1=0,
解得q=
-1,
故公比q的取值集合为{
-1},
故答案为:{
-1}
ak-(ak+1+ak+2)qk•(
| 1 |
| q |
要使仍是该数列中的一项,则
| 1 |
| q |
∵0<q<
| 1 |
| 2 |
| 1 |
| q |
| 1 |
| 2 |
即q0=1或qn<
| 1 |
| 2 |
∴
| 1 |
| q |
即q2+2q-1=0,
解得q=
| 2 |
故公比q的取值集合为{
| 2 |
故答案为:{
| 2 |

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
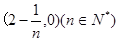 且方向向量为
且方向向量为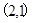 的直线交椭圆
的直线交椭圆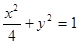 于
于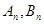 两点,记原点为
两点,记原点为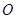 ,
,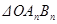 面积为
面积为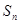 ,则
,则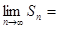 _______
_______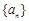 满足
满足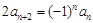 ,且
,且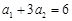 ,则
,则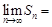
 .
.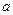 满足
满足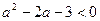 ,则
,则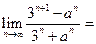 ____________.
____________.