Question

【题目】已知椭圆的左焦点为F1 ， 右焦点为F2 ． 若椭圆上存在一点P，满足线段PF2相切于以椭圆的短轴为直径的圆，切点为线段PF2的中点，则该椭圆的离心率为（ ）
A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：如图， 设以椭圆的短轴为直径的圆与线段PF2相切于M点，连接OM，PF2；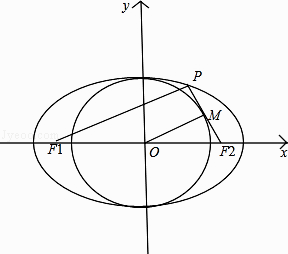

∵M，O分别是PF2 ， F1F2的中点；
∴MO∥PF1 ， 且|PF1|=2|MO|=2b；
OM⊥PF2；
∴PF1⊥PF2 ， |F1F2|=2c；
∴ ；
根据椭圆的定义，|PF1|+|PF2|=2a；
∴ ；
∴ ；
两边平方得：a2﹣2ab+b2=c2﹣b2 ， c2=a2﹣b2代入并化简得：
2a=3b，∴ ；
∴ ；
即椭圆的离心率为 ．
故选A．