题目内容
【题目】已知函数 
有两个零点．
（1）若函数的两个零点是 
和 
，求 
的值；
（2）若函数的两个零点是 
和 
，求 
的取值范围．
【答案】
（1）解：∵ 
和 
是函数 
的两个零点，
∴ 和 是方程 
的两个实数根．
则 
解得 
（2）解：∵函数的两个零点为 
和 
，
∴ 和 是方程 的两根，
∴ 
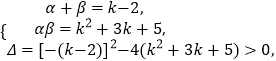
则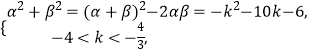 
∴ 
的取值范围为 
.
【解析】(1)根据零点的定义代入数值求出k的值即可。(2)利用零点的定义再结合二次函数的根的情况得到关于
的不等式组，整理为关于k的二次函数由二次函数在指定区间上的最值情况即可得出取值范围。
【考点精析】解答此题的关键在于理解函数的零点的相关知识，掌握函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点．
练习册系列答案
小学教材完全解读系列答案
相关题目
【题目】设y=f（t）是某港口水的深度y（米）关于时间t（时）的函数，其中0≤t≤24．下表是该港口某一天从0时至24时记录的时间t与水深y的关系表：
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 5 | 7.5 | 5 | 2.5 | 5 | 7.5 | 5 | 2.5 | 5 |
经长期观察，函数y=f（t）的图象可以近似地看成函数y=k+Asin（ωt+φ）的图象．下面的函数中，最能近似表示表中数据间对应关系的函数是（ ）
A.
B.
C.
D.
