题目内容
在直角坐标平面中,已知点P1(1,2),P2(2,22),P3(3,23),…,Pn(n,2n),其中n是正整数,对平面上任一点A0,记A1为A0关于点P1的对称点,A2为A1关于点P2的对称点,……,An为An-1关于点Pn的对称点,
(1)求向量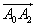 的坐标;
的坐标;
(2)当点A0在曲线C上移动时,点A2的轨迹是函数y=f(x)的图象,其中f(x)是以3为周期的周期函数,且当x∈(0,3]时,f(x)=lgx,求以曲线C为图象的函数在(1,4]上的解析式;
(3)对任意偶数n,用n表示向量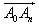 的坐标。
的坐标。
(1)求向量
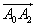 的坐标;
的坐标;(2)当点A0在曲线C上移动时,点A2的轨迹是函数y=f(x)的图象,其中f(x)是以3为周期的周期函数,且当x∈(0,3]时,f(x)=lgx,求以曲线C为图象的函数在(1,4]上的解析式;
(3)对任意偶数n,用n表示向量
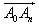 的坐标。
的坐标。解:(1)设点 ,A0关于点P1的对称点A1的坐标为
,A0关于点P1的对称点A1的坐标为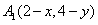 ,
,
A1关于点P2的对称点A2的坐标为 ,
,
所以,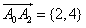 ;
;
(2)∵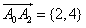 ,
,
∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到,
因此,曲线C是函数y=g(x)的图象,其中g(x)是以3为周期的周期函数,
且当x∈(-2,1]时, ,
,
于是当x∈(1,4]时,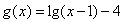 ;
;
(3)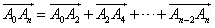 ,
,
由于 ,
,
得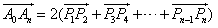
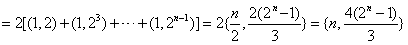 。
。

练习册系列答案
相关题目
 的坐标;
的坐标; ,
, ,对平面上任意一点
,对平面上任意一点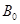 ,记
,记 为
为 的对称点,
的对称点, 为
为 的对称点,
的对称点, 为
为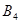 为
为 为
为 关于
关于 为
为 为
为 …。则
…。则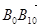 =
=