题目内容
在直角坐标平面中,已知点P(0,1),Q(2,3),对平面上任意一点B0,记B1为B0关于P的对称点,B2为B1关于Q的对称点,B3为B2关于P的对称点,B4为B3关于Q的对称点,…,Bi为Bi-1关于P的对称点,Bi+1为Bi关于Q的对称点,Bi+2为Bi+1关于P的对称点(i≥1,i∈N)….则
=
| B0B10 |
(20,20)
(20,20)
.分析:由题意可得,
=
+
=2
+2
=2
,同理可得
=2
,
=2
,
=2
,
=2
,把这5个等式相加可得
的坐标.
| B0B2 |
| B0B1 |
| B1B2 |
| PB1 |
| B1Q |
| PQ |
| B2B4 |
| PQ |
| B4B6 |
| PQ |
| B6B8 |
| PQ |
| B8B10 |
| PQ |
| B0B10 |
解答:解:由题意可得,
=
+
=2
+2
=2
,
=
+
=2
+2
=2
,
同理可得
=2
,
=2
,
=2
,
把这5个等式相加可得
=10
=(20,20).
故答案为:(20,20).
| B0B2 |
| B0B1 |
| B1B2 |
| PB1 |
| B1Q |
| PQ |
| B2B4 |
| B2B3 |
| B3B4 |
| PB3 |
| B3Q |
| PQ |
同理可得
| B4B6 |
| PQ |
| B6B8 |
| PQ |
| B8B10 |
| PQ |
把这5个等式相加可得
| B0B10 |
| PQ |
故答案为:(20,20).
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,属于基础题.

练习册系列答案
相关题目
 的坐标;
的坐标; ,
, ,对平面上任意一点
,对平面上任意一点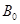 ,记
,记 为
为 的对称点,
的对称点, 为
为 的对称点,
的对称点, 为
为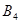 为
为 为
为 关于
关于 为
为 为
为 …。则
…。则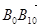 =
=