题目内容
在直角坐标平面中,已知点P1(1,2),P2(2,22),P3(3,23),…,Pn(n,2n),其中n是正整数.对平面上任一点A0,记A1为A0关于点P1的对称点,A2为A1关于点P2的对称点,…,An为An-1关于点Pn的对称点.(1)求向量
| A0A2 |
(2)当点A0在曲线C上移动时,点A2的轨迹是函数y=f(x)的图象,其中f(x)是以3位周期的周期函数,且当x∈(0,3]时,f(x)=lgx.求以曲线C为图象的函数在(1,4]上的解析式;
(3)对任意偶数n,用n表示向量
| A0An |
分析:(1)利用中点坐标公式求出点A1,A2的坐标,再利用向量的坐标公式求出
的坐标.
(2)由已知判断出y=f(x)的图象是由C按
平移得到的;得到C是由f(x)左移两个单位,下移4个单位得到,利用图象变换求出C的解析式.
(3)利用向量的运算法则将
有以Pn为起点终点的向量表示,利用向量的坐标公式求出各向量的坐标,利用等比数列的前n项和公式求出向量的坐标.
| A0A2 |
(2)由已知判断出y=f(x)的图象是由C按
| A0A2 |
(3)利用向量的运算法则将
| A0An |
解答:解:(1)设点A0(x,y),A1为A0关于点P1的对称点,A1的坐标为(2-x,4-y),
A1为P2关于点的对称点A2的坐标为(2+x,4+y),
∴
={2,4}.
(2)∵
={2,4},
∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到.
因此,设曲线C是函数y=g(x)的图象,
其中g(x)是以3为周期的周期函数,
且当x∈(-2,1]时,g(x)=lg(x+2)-4.
于是,当x∈(1,4]时,g(x)=lg(x-1)-4.
(3)
=
+
+…+
,
由于
=2
,得
=2(
+
+…+
)
=2({1,2}+{1,23}+…+{1,2n-1})=2{
,
}={n,
}
A1为P2关于点的对称点A2的坐标为(2+x,4+y),
∴
| A0A2 |
(2)∵
| A0A2 |
∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到.
因此,设曲线C是函数y=g(x)的图象,
其中g(x)是以3为周期的周期函数,
且当x∈(-2,1]时,g(x)=lg(x+2)-4.
于是,当x∈(1,4]时,g(x)=lg(x-1)-4.
(3)
| A0An |
| A0A2 |
| A2A4 |
| An-2An |
由于
| A2k-2A2k |
| P2k-1P2k |
| A0An |
| P1P2 |
| P3P4 |
| Pn-1Pn |
=2({1,2}+{1,23}+…+{1,2n-1})=2{
| n |
| 2 |
| 2(2n-1) |
| 3 |
| 4(2n-1) |
| 3 |
点评:本题考查中点坐标公式、向量的坐标公式、图象的平移变换、等比数列的前n项和公式.

练习册系列答案
相关题目
 的坐标;
的坐标; ,
, ,对平面上任意一点
,对平面上任意一点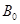 ,记
,记 为
为 的对称点,
的对称点, 为
为 的对称点,
的对称点, 为
为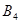 为
为 为
为 关于
关于 为
为 为
为 …。则
…。则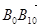 =
=