题目内容
11.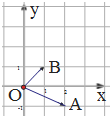 如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,设复数$z=\frac{z_1}{z_2}$,则z的共轭复数为( )
如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,设复数$z=\frac{z_1}{z_2}$,则z的共轭复数为( )| A. | $\frac{1}{2}-\frac{3}{2}i$ | B. | $\frac{1}{2}+\frac{3}{2}i$ | C. | 1-3i | D. | 1+3i |
分析 由题意结合图形求出z1=2-i,z2=1+i,代入$z=\frac{z_1}{z_2}$,由复数代数形式的乘除运算化简,再由共轭复数的概念得答案.
解答 解:由图可知,z1=2-i,z2=1+i,
∴$z=\frac{{z}_{1}}{{z}_{2}}=\frac{2-i}{1+i}=\frac{(2-i)(1-i)}{(1+i)(1-i)}$=$\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i$,
∴$\overline{z}=\frac{1}{2}+\frac{3}{2}i$.
故选:B.
点评 本题考查复数的代数表示法及其几何意义,考查了复数代数形式的乘除运算,是基础题.

练习册系列答案
相关题目
19.已知xy=$\frac{1}{9}$,0<x<y<1,u=log${\;}_{\frac{1}{3}}$xlog${\;}_{\frac{1}{3}}$y,则( )
| A. | u≤1 | B. | u<1 | C. | u>1 | D. | u≥1 |