题目内容
5.在等差数列{an}中,首项a1=1,数列{bn}满足bn=($\frac{1}{2}$)an,b1b2b3=$\frac{1}{64}$(I)求数列{an}的通项公式;
(Ⅱ)求a1b1+a2b2+…+anbn<2.
分析 (I)通过b1=$\frac{1}{2}$、b2=$\frac{1}{{2}^{1+d}}$、b3=$\frac{1}{{2}^{1+2d}}$,利用b1b2b3=$\frac{1}{64}$计算即得结论;
(Ⅱ)通过an=n可知anbn=n•$\frac{1}{{2}^{n}}$,利用错位相减法计算即得结论.
解答 (I)解:设等差数列{an}的公差为d,
依题意,b1=$\frac{1}{2}$,b2=$\frac{1}{{2}^{1+d}}$,b3=$\frac{1}{{2}^{1+2d}}$,
∵b1b2b3=$\frac{1}{64}$,
∴$\frac{1}{2}$•$\frac{1}{{2}^{1+d}}$•$\frac{1}{{2}^{1+2d}}$=$\frac{1}{{2}^{6}}$,
∴1+(1+d)+(1+2d)=6,
解得:d=1,
∴an=1+(n-1)=n;
(Ⅱ)证明:∵an=n,∴bn=$\frac{1}{{2}^{n}}$,
anbn=n•$\frac{1}{{2}^{n}}$,
记Tn=a1b1+a2b2+…+anbn=1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+3•$\frac{1}{{2}^{3}}$+…+n•$\frac{1}{{2}^{n}}$,
则$\frac{1}{2}•$Tn=1•$\frac{1}{{2}^{2}}$+2•$\frac{1}{{2}^{3}}$+…+(n-1)•$\frac{1}{{2}^{n}}$+n•$\frac{1}{{2}^{n+1}}$,
两式相减得:$\frac{1}{2}•$Tn=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-n•$\frac{1}{{2}^{n+1}}$
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n+1}}$
=1-$\frac{1}{{2}^{n}}$-n•$\frac{1}{{2}^{n+1}}$,
∴Tn=2(1-$\frac{1}{{2}^{n}}$-n•$\frac{1}{{2}^{n+1}}$)=2-$\frac{1}{{2}^{n-1}}$-$\frac{n}{{2}^{n}}$,
∵2-$\frac{1}{{2}^{n-1}}$-$\frac{n}{{2}^{n}}$<2,
∴a1b1+a2b2+…+anbn<2.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | (-3,-1) | B. | (-3,1) | C. | (-1,0) | D. | (-1,2) |
| A. | 零向量是唯一没有方向的向量 | |
| B. | 平面内的单位向量有且仅有一个 | |
| C. | $\overrightarrow{a}$与$\overrightarrow{b}$是共线向量,$\overrightarrow{b}$与$\overrightarrow{c}$是平行向量,则$\overrightarrow{a}$与$\overrightarrow{c}$是方向相同的向量 | |
| D. | 相等的向量必是共线向量 |
| A. | 命题“若x<1,则-≤x≤1”的逆否命题是“若x≥1,则x<-1或x≥1” | |
| B. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0” | |
| C. | “a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件 | |
| D. | 已知命题p:?x∈R,lnx<lgx;命题q:?x0∈R,x03=1-x02,则“(¬p)∨(¬q)为真命题”. |
| A. | 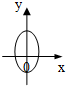 | B. | 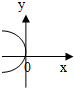 | C. | 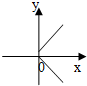 | D. | 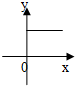 |