题目内容
【题目】已知直线l经过点![]() .
.
(1)若直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)若![]() ,
,![]() 两点到直线
两点到直线![]() 的距离相等,求直线
的距离相等,求直线![]() 的方程.
的方程.
【答案】(1)![]() 或
或![]() (2)
(2)![]() 或
或![]()
【解析】
(1)讨论直线是否过原点,利用截距相等进行求解即可.
(2)根据点到直线的距离相等,分直线平行和直线过A,B的中点两种情况进行求解即可.
(1)若直线过原点,则设为y=kx,则k=2,此时直线方程为y=2x,
当直线不过原点,设方程为![]() 1,即x+y=a,
1,即x+y=a,
此时a=1+2=3,则方程为x+y=3,
综上直线方程为y=2x或x+y=3.
(2)若A,B两点在直线l同侧,
则AB∥l,
AB的斜率k![]() 1,
1,
即l的斜率为1,
则l的方程为y﹣2=x﹣1,即y=x+1,
若A,B两点在直线的两侧,即l过A,B的中点C(2,0),
则k![]() 2,
2,
则l的方程为y﹣0=﹣2(x﹣2),即y=﹣2x+4,
综上l的方程为y=﹣2x+4或y=x+1.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案【题目】在某次测试中,卷面满分为100分,考生得分为整数,规定60分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响,对午休和不午休的考生进行了测试成绩的统计,数据如下表:

(1)根据上述表格完成下列列联表:

(2)判断“能否在犯错误的概率不超过0.010的前提下认为成绩及格与午休有关”?
(参考公式:![]() ,其中
,其中![]() .)
.)
| 0.010 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
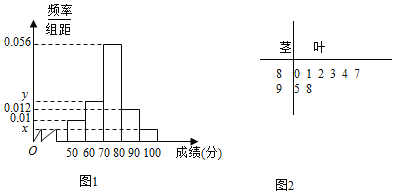
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.