题目内容
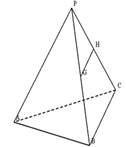
在四棱锥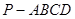 中,
中,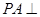 平面
平面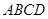 ,底面
,底面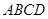 为矩形,
为矩形,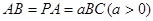 .
.
(Ⅰ)当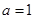 时,求证:
时,求证: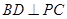 ;
;
(Ⅱ)若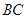 边上有且只有一个点
边上有且只有一个点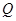 ,使得
,使得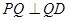 ,求此时二面角
,求此时二面角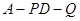 的余弦值.
的余弦值.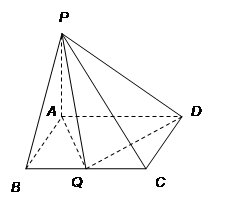
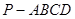 中,
中,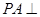 平面
平面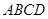 ,底面
,底面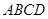 为矩形,
为矩形,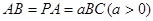 .
.(Ⅰ)当
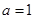 时,求证:
时,求证: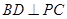 ;
;(Ⅱ)若
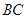 边上有且只有一个点
边上有且只有一个点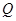 ,使得
,使得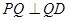 ,求此时二面角
,求此时二面角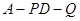 的余弦值.
的余弦值.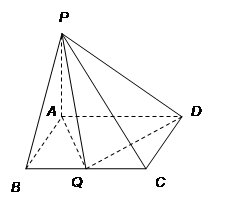
(1)见解析:(2)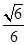 .
.
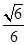 .
.本试题主要考查了立体几何中线线垂直和二面角的求解运用。
解:(Ⅰ)当嗄时,底面ABCD为正方形,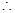 BD
BD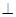 AC
AC
又因为BD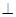 PABD,
PABD,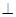 面PAC…………………………2分
面PAC…………………………2分
又PC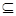 面PAC
面PAC
BD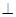 PC…………………………3分
PC…………………………3分

(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线
为X轴、Y轴、Z轴建立坐标系,如图所示,
则
B(1,0,0)D(0,a,0)C(1,a,0)P(0,0,1)…………………4分
设BQ=m,则Q(1,m,0)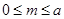
要使PQ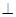 QD,只要-1+m(a-m)=0
QD,只要-1+m(a-m)=0
所以1=m(a-m)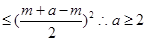 ,……6分
,……6分
由此可知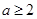
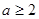 时,存在点Q使得PQ
时,存在点Q使得PQ QD
QD
当且仅当m= a-m,即m=a/2时,BC边上有且只有一个点Q,使得PQ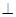 QD
QD
由此可知a=2…………………………8分
设面PDQ的法向量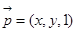
则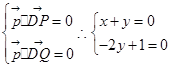 解得
解得 …………………………10分
…………………………10分
取平面PAD的法向量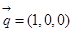
则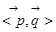 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以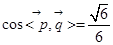
因此二面角A-PD-Q的余弦值为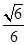 …………………………12分
…………………………12分
解:(Ⅰ)当嗄时,底面ABCD为正方形,
 BD
BD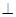 AC
AC又因为BD
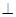 PABD,
PABD,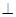 面PAC…………………………2分
面PAC…………………………2分又PC
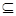 面PAC
面PACBD
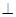 PC…………………………3分
PC…………………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线
为X轴、Y轴、Z轴建立坐标系,如图所示,
则
B(1,0,0)D(0,a,0)C(1,a,0)P(0,0,1)…………………4分
设BQ=m,则Q(1,m,0)
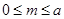
要使PQ
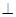 QD,只要-1+m(a-m)=0
QD,只要-1+m(a-m)=0所以1=m(a-m)
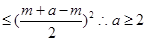 ,……6分
,……6分由此可知
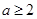
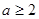 时,存在点Q使得PQ
时,存在点Q使得PQ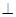 QD
QD当且仅当m= a-m,即m=a/2时,BC边上有且只有一个点Q,使得PQ
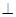 QD
QD由此可知a=2…………………………8分
设面PDQ的法向量
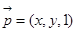
则
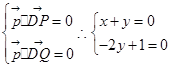 解得
解得 …………………………10分
…………………………10分取平面PAD的法向量
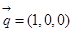
则
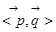 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以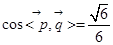
因此二面角A-PD-Q的余弦值为
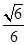 …………………………12分
…………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
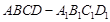 中,
中,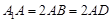 ,
,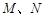 分别是
分别是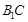 、
、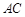 中点。
中点。 ;
; 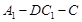 的正切值。
的正切值。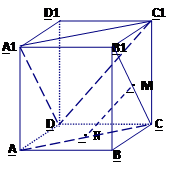
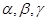 ,三条直线a,b,c共点,知:
,三条直线a,b,c共点,知: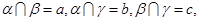 且
且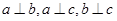 。求证:
。求证: 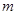 ,
,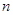 为两条不同的直线,
为两条不同的直线,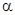 ,
,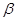 为两个不同的平面,则下列命题是真命题的是( )
为两个不同的平面,则下列命题是真命题的是( )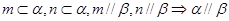
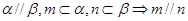
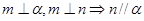
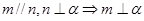
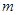 、
、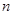 为不同的两条直线),
为不同的两条直线),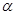 、
、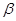 为不同的两个平面)
为不同的两个平面)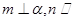
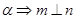
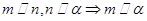
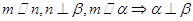
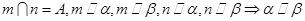
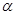 、
、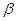 是两个不同的平面,则下列说法正确的是
是两个不同的平面,则下列说法正确的是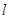 ,
,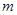 是两条不同的直线,
是两条不同的直线,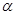 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( ) ,
, ,则
,则
 ,则
,则
 ,
, ,则
,则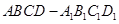 的底面是直角梯形,
的底面是直角梯形,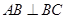 ,
,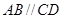 ,
, ,
,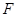 分别是棱
分别是棱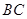 ,
,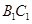 上的动点,且
上的动点,且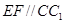 ,
,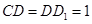 ,
,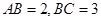 .
.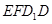 都为矩形;
都为矩形;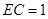 时,求几何体
时,求几何体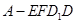 的体积。
的体积。