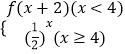题目内容
【题目】下表是一位母亲给儿子作的成长记录：
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
根据以上样本数据，她建立了身高 
（cm）与年龄x（周岁）的线性回归方程为 
，给出下列结论：
①y与x具有正的线性相关关系；
②回归直线过样本的中心点（42，117.1）；
③儿子10岁时的身高是 
cm；
④儿子年龄增加1周岁，身高约增加 
cm.
其中，正确结论的个数是
A.1
B.2
C.3
D.4
【答案】B
【解析】解答线性回归方程为 
=7.19 
+73.93， ①7.19＞0，即y随x的增大而增大，y与x具有正的线性相关关系，①正确；
②回归直线过样本的中心点为（6，117.1），②错误；
③当x=10时， =145.83，此为估计值，所以儿子10岁时的身高的估计值是145.83cm而不一定是实际值，③错误；
④回归方程的斜率为7.19，则儿子年龄增加1周岁，身高约增加7.19cm，④正确，
故应选：B
分析：本题主要考查了回归分析的初步应用，解决问题的关键是根据回归分析的原理分析判断即可.
练习册系列答案
相关题目
【题目】假设关于某设备的使用年限x和支出的维修费用y（万元），有如下表的统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系，试求：
（1）线性回归方程 
.
（2）估计使用年限为10年时，维修费用是多少.
（3）计算总偏差平方和、残差平方和及回归平方和.
（4）求 
并说明模型的拟合效果.
