题目内容
在边长为10的正方形 内有一动点
内有一动点 ,
, ,作
,作 于
于 ,
, 于
于 ,求矩形
,求矩形 面积的最小值和最大值,并指出取最大值时
面积的最小值和最大值,并指出取最大值时 的具体位置.
的具体位置.
最小值为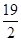 ;最大值为
;最大值为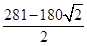 ,此时
,此时 点处在
点处在 的角平分线上,且满足
的角平分线上,且满足 .
.
解析试题分析:本题是函数模型的建立与应用问题,解题的关键是引入适当的变量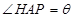 ,建立面积
,建立面积 与
与 的三角函数模型
的三角函数模型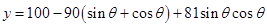 ,然后根据同角三角函数的基本关系式,令
,然后根据同角三角函数的基本关系式,令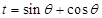 ,再将模型转化为关于
,再将模型转化为关于 的二次函数
的二次函数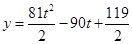 模型,转化时要特别注意变量取值范围的变化,最后利用二次函数的性质求取函数的最值,并确定取得最大值点
模型,转化时要特别注意变量取值范围的变化,最后利用二次函数的性质求取函数的最值,并确定取得最大值点 的位置.
的位置.
试题解析:连结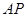 ,延长
,延长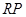 交
交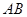 于
于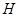 ,设
,设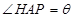
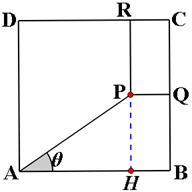
则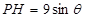 ,
,
设矩形 的面积为
的面积为 ,则
,则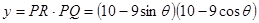
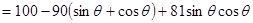 4分
4分
设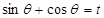 ,则
,则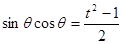
又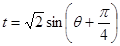 ,
,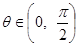
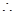
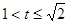
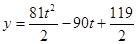
 (
(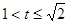 ) 8分
) 8分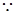
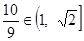
 当
当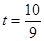 时,
时,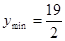 10分
10分
当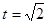 时,
时,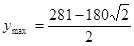
此时,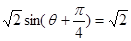 ,又
,又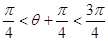
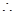
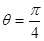 13分.
13分.
考点:1.函数的应用;2.二次函数的最值;3.三角函数的性质.

练习册系列答案
相关题目
 (
( 为常数,且
为常数,且 ).
). 时,求函数
时,求函数 的最小值(用
的最小值(用 使得
使得 ,
, ,并且
,并且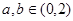 ,若存在,求出实数
,若存在,求出实数 与听课时间
与听课时间 (单位:分钟)之间的关系满足如图所示的图像,当
(单位:分钟)之间的关系满足如图所示的图像,当 时,图像是二次函数图像的一部分,其中顶点
时,图像是二次函数图像的一部分,其中顶点 ,过点
,过点 ;当
;当 时,图像是线段
时,图像是线段 ,其中
,其中 ,根据专家研究,当注意力指数大于62时,学习效果最佳.
,根据专家研究,当注意力指数大于62时,学习效果最佳.
 的函数关系式;
的函数关系式; 是偶函数
是偶函数 的图象与直线
的图象与直线 没有交点,求b的取值范围;
没有交点,求b的取值范围; ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围
的取值范围 满足
满足 ,且
,且 .
. 时,函数
时,函数 的图像恒在函数
的图像恒在函数 的图像的上方,求实数
的图像的上方,求实数 的取值范围.
的取值范围. ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称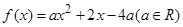 ,试判断
,试判断 上的“局部奇函数”?若是,求出满足
上的“局部奇函数”?若是,求出满足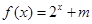 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; 为定义域
为定义域 的定义域为
的定义域为 ,且
,且 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 .
. ,
, ,判断
,判断 ,并说明理由;
,并说明理由; 若
若 ,
, 且
且 ,函数
,函数 .
. ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
. 的解析式和值域;
的解析式和值域; 时,数列
时,数列 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有
 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由. .
. 的定义域;
的定义域; 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.