题目内容
P为圆A: 上的动点,点
上的动点,点 .线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
.线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
(1)求曲线Γ的方程;
(2)当点P在第一象限,且 时,求点M的坐标.
时,求点M的坐标.
 上的动点,点
上的动点,点 .线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
.线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.(1)求曲线Γ的方程;
(2)当点P在第一象限,且
 时,求点M的坐标.
时,求点M的坐标.(1)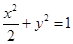 ;(2)
;(2)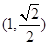 .
.
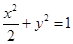 ;(2)
;(2)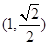 .
.试题分析:本题主要考查椭圆的定义和标准方程、圆的方程、直线的方程、直线与曲线的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力. 第一问,根据圆的方程得到圆心A的坐标和半径的长,利用垂直平分线得到
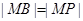 ,而
,而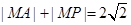 ,所以
,所以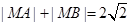 ,根据椭圆的定义,判断点M的轨迹为椭圆,得到椭圆的标准方程;根据已知条件先得出P点坐标,从而得到直线AP的方程,利用直线与椭圆相交解出M点坐标,过程中应注意方程根的取舍.
,根据椭圆的定义,判断点M的轨迹为椭圆,得到椭圆的标准方程;根据已知条件先得出P点坐标,从而得到直线AP的方程,利用直线与椭圆相交解出M点坐标,过程中应注意方程根的取舍.试题解析:(1)圆
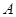 的圆心为
的圆心为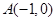 ,半径等于
,半径等于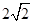 .
.由已知
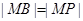 ,于是
,于是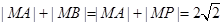 ,
,故曲线Γ是以
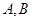 为焦点,以
为焦点,以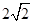 为长轴长的椭圆,
为长轴长的椭圆,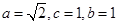 ,
,曲线Γ的方程为
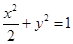 . 5分
. 5分(2)由
 ,
,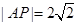 ,得
,得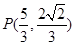 . 8分
. 8分于是直线
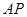 方程为
方程为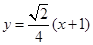 .
.由
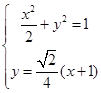 解得
解得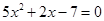 ,
,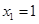 ,
,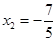 .
.由于点
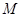 在线段
在线段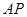 上,所以点
上,所以点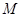 坐标为
坐标为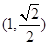 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
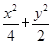 =1的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
=1的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
 ,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ=
,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ= .
.
 :
: 的切线l,切点A在第二象限。
的切线l,切点A在第二象限。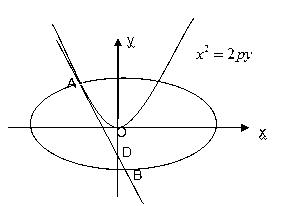
 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k, ,①试用斜率k表示
,①试用斜率k表示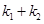 ②当
②当 是椭圆
是椭圆 的半焦距,则
的半焦距,则 的取值范围为 .
的取值范围为 . ,
, 是椭圆长轴的一个端点,
是椭圆长轴的一个端点, 是椭圆短轴的一个端点,
是椭圆短轴的一个端点, 为椭圆的一个焦点.若
为椭圆的一个焦点.若 ,则该椭圆的离心率为 ( )
,则该椭圆的离心率为 ( )






 右支上的一点,M,N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
右支上的一点,M,N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )