题目内容
（2012•包头一模）若点O和点F分别为双曲线
-
=1的中心和左焦点，点P为双曲线右支上的任意一点，则
•
的最小值为（ ）
| x2 |
| 4 |
| y2 |
| 5 |
| OP |
| FP |
分析：设P（x，y）（x≥2），则先利用向量的数量积的坐标表示求出
•
，然后利用二次函数的性质即可求解最小值
| OP |
| FP |
解答：解：设P（x，y）（x≥2）
由题意可得，F（-3，0），O（0，0），
=(x，y)，
=(x+3，y)
∴
•
=x2+3x+y2=x2+3x+
-5=
+3x-5（x≥2）
结合二次函数的性质可知，当x=2时，f（x）有最小值10
故选D
由题意可得，F（-3，0），O（0，0），
| OP |
| FP |
∴
| OP |
| FP |
| 5x2 |
| 4 |
| 9x2 |
| 4 |
结合二次函数的性质可知，当x=2时，f（x）有最小值10
故选D
点评：本题以向量的数量积的坐标表示为载体，主要考查了双曲线的范围及二次函数的性质的综合应用
练习册系列答案
步步高达标卷系列答案
相关题目
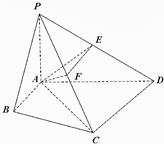（2012•包头一模）在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2，AB=1．
（2012•包头一模）函数f（x）=sin（ωx+?）（其中