题目内容
【题目】如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且 ![]() =λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.
=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示. 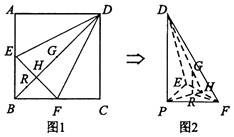
(I)若λ=2,求证:GR⊥平面PEF;
(Ⅱ)是否存在正实数λ,使得直线FR与平面DEF所成角的正弦值为 ![]() ?若存在,求出λ的值;若不存在,请说明理由.
?若存在,求出λ的值;若不存在,请说明理由.
【答案】(I)证明:由题意,PE,PF,PD三条直线两两垂直,∴PD⊥平面PEF, 图1中,EF∥AC,∴GB=2GH,
∵G为BD中点,∴DG=2GH.
图2中,∵ ![]() =2,∴△PDH中,GR∥PD,
=2,∴△PDH中,GR∥PD,
∴GR⊥平面PEF;
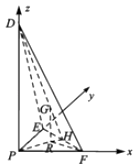
(Ⅱ)解:由题意,建立如图所示的坐标系,设PD=4,则P(0,0,0),F(2,0,0),E(0,2,0),D(0,0,4),∴H(1,1,0),
∵ ![]() =λ,∴R(
=λ,∴R( ![]() ,
, ![]() ,0),
,0),
∴ ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,0),
,0),
∵ ![]() =(2,﹣2,0),
=(2,﹣2,0), ![]() =(0,2,﹣4),
=(0,2,﹣4),
设平面DEF的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则 ![]() ,取
,取 ![]() =(2,2,1),
=(2,2,1),
∵直线FR与平面DEF所成角的正弦值为 ![]() ,
,
∴ 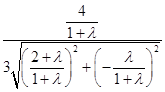 =
= ![]() ,
,
∴λ= ![]() ,
,
∴存在正实数λ= ![]() ,使得直线FR与平面DEF所成角的正弦值为
,使得直线FR与平面DEF所成角的正弦值为 ![]() .
.
【解析】(I)若λ=2,证明PD⊥平面PEF,GR∥PD,即可证明:GR⊥平面PEF;(Ⅱ)建立如图所示的坐标系,求出平面DEF的一个法向量,利用直线FR与平面DEF所成角的正弦值为 ![]() ,建立方程,即可得出结论.
,建立方程,即可得出结论.
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则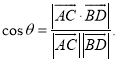 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
