题目内容
【题目】设函数f(x)=2x﹣cosx,{an}是公差为 ![]() 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则 ![]() =( )
=( )
A.0
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵f(x)=2x﹣cosx,
∴f(a1)+f(a2)+…+f(a5)=2(a1+a2+…+a5)﹣(cosa1+cosa2+…+cosa5),
∵{an}是公差为 ![]() 的等差数列,
的等差数列,
∴a1+a2+…+a5=5a3 , 由和差化积公式可得,
cosa1+cosa2+…+cosa5
=(cosa1+cosa5)+(cosa2+cosa4)+cosa3
=[cos(a3﹣ ![]() ×2)+cos(a3+
×2)+cos(a3+ ![]() ×2)]+[cos(a3﹣
×2)]+[cos(a3﹣ ![]() )+cos(a3+
)+cos(a3+ ![]() )]+cosa3
)]+cosa3
=2cos ![]() cos
cos ![]() +2cos
+2cos ![]() cos
cos ![]() +cosa3
+cosa3
=2cosa3 ![]() +2cosa3cos(﹣
+2cosa3cos(﹣ ![]() )+cosa3
)+cosa3
=cosa3(1+ ![]() +
+ ![]() ),
),
∵f(a1)+f(a2)+…+f(a5)=5π,
∴10a3﹣cosa3(1+ ![]() +
+ ![]() )=5π,
)=5π,
∴cosa3=0,10a3=5π,
故a3= ![]() ,
,
∴ ![]()
=π2﹣( ![]() ﹣
﹣ ![]() )
) ![]()
=π2﹣ ![]()
= ![]() .
.
故选D.

 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析,为了考察甲球员对球队的贡献,现作如下数据统计:
球队胜 | 球队负 | 总计 | |
甲参加 | 22 | b | 30 |
甲未参加 | c | 12 | d |
总计 | 30 | e | n |
(1)求b,c,d,e,n的值,据此能否有97.7%的把握认为球队胜利与甲球员参赛有关;
(2)根据以往的数据统计,乙球员能够胜任前锋、中锋、后卫以及守门员四个位置,且出场率分别为:0.2,0.5,0.2,0.1,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:0.4,0.2,0.6,0.2.则:
当他参加比赛时,求球队某场比赛输球的概率;
当他参加比赛时,在球队输了某场比赛的条件下,求乙球员担当前锋的概率;
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 7.879 | 10.828 |
![]() .
.
【题目】随着互联网的迅速发展,越来越多的消费者开始选择网络购物这种消费方式某营销部门统计了2019年某月锦州的十大特产的网络销售情况得到网民对不同特产的最满意度![]() 和对应的销售额
和对应的销售额![]() (万元)数据,如下表:
(万元)数据,如下表:
特产种类 | 甲 | 乙 | 丙 | 丁 | 戊 | 已 | 庚 | 辛 | 壬 | 癸 |
最满意度 |
|
|
|
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
|
|
|
![]() 求销量额
求销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() ;
;
![]() 我们约定:销量额
我们约定:销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() 的绝对值在
的绝对值在![]() 以上(含
以上(含![]() )是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额
)是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额![]() 关于最满意度
关于最满意度![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ).
).
参考数据:![]()
![]() ,
,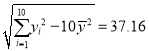 ,
,![]() ,
,![]() .
.
附:对于一组数据![]() .其回归直线方程
.其回归直线方程![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: ,
,![]() .线性相关系数
.线性相关系数
【题目】某种农作物可以生长在滩涂和盐碱地,它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度![]() 对亩产量
对亩产量![]() (吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表:
(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
残差 |
|
|
|
|
|
绘制散点图发现,可以用线性回归模型拟合亩产量![]() (吨)与海水浓度
(吨)与海水浓度![]() 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
(1)求![]() 的值;
的值;
(2)统计学中常用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,回归效果越好,如假设
越大,回归效果越好,如假设![]() ,就说明预报变量
,就说明预报变量![]() 的差异有
的差异有![]() 是解释变量
是解释变量![]() 引起的.请计算相关指数
引起的.请计算相关指数![]() (精确到
(精确到![]() ),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
(附:残差![]() ,相关指数
,相关指数 ,其中
,其中![]() )
)
【题目】随着共享单车的蓬勃发展,越来越多的人将共享单车作为短距离出行的交通工具.为了解不同年龄的人们骑乘单车的情况,某共享单车公司对某区域不同年龄的骑乘者进行了调查,得到数据如下:
年龄 | 15 | 25 | 35 | 45 | 55 | 65 |
骑乘人数 | 95 | 80 | 65 | 40 | 35 | 15 |
(1)求![]() 关于
关于![]() 的线性回归方程,并估计年龄为40岁人群的骑乘人数;
的线性回归方程,并估计年龄为40岁人群的骑乘人数;
(2)为了回馈广大骑乘者,该公司在五一当天通过![]() 向每位骑乘者的前两次骑乘分别随机派送一张面额为1元,或2元,或3元的骑行券.已知骑行一次获得1元券,2元券,3元券的概率分别是
向每位骑乘者的前两次骑乘分别随机派送一张面额为1元,或2元,或3元的骑行券.已知骑行一次获得1元券,2元券,3元券的概率分别是![]() ,
,![]() ,
,![]() ,且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车,记该骑乘者当天获得的骑行券面额之和为
,且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车,记该骑乘者当天获得的骑行券面额之和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.


