题目内容
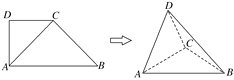
【题目】(2017·郑州第二次质量预测)如图，高为1的等腰梯形ABCD中，AM＝CD＝
AB＝1.现将△AMD沿MD折起，使平面AMD⊥平面MBCD，连接AB，AC.
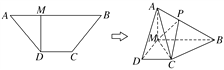
(1)在AB边上是否存在点P，使AD∥平面MPC?
(2)当点P为AB边的中点时，求点B到平面MPC的距离．
【答案】（1）见解析（2）
【解析】试题分析:(1) 连接BD交MC于点N，则
,因此AP＝
AB ,再根据线面平行判定定理得结论(2)利用等体积法
,再根据AM⊥平面MBCD,得
,最后计算三角形面积代入可得结果
试题解析:解：(1)当AP＝
AB时，有AD∥平面MPC.
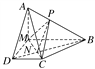
理由如下：
连接BD交MC于点N，连接NP.
在梯形MBCD中，DC∥MB，
＝
＝
，
在△ADB中，
＝，∴AD∥PN.
∵AD平面MPC，PN平面MPC，
∴AD∥平面MPC.
(2)∵平面AMD⊥平面MBCD，平面AMD∩平面MBCD＝DM，AM⊥DM，∴AM⊥平面MBCD.
∴VPMBC＝×S△MBC×
＝××2×1×＝
.
在△MPC中，MP＝AB＝
，MC＝
，
又PC＝
＝，
∴S△MPC＝××
＝
.
∴点B到平面MPC的距离为
d＝
＝
＝
.
练习册系列答案
相关题目
