题目内容
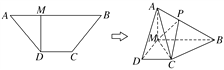
【题目】如图,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=![]() AB=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC.
AB=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC.
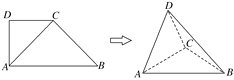
(1)求证:AD⊥平面BCD;
(2)求三棱锥CABD的高.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先根据勾股定理得AC⊥BC. 再根据面面垂直性质定理得BC⊥平面ACD,即得AD⊥BC. 最后根据线面垂直判定定理得结论(2)因为BC⊥平面ACD,所以根据等体积法以及锥体体积公式即得结果
试题解析:解:(1)证明:由已知得AC=2![]() ,BC=2
,BC=2![]() ,又AB=4,∴AC2+BC2=AB2,∴AC⊥BC.
,又AB=4,∴AC2+BC2=AB2,∴AC⊥BC.
又∵平面ADC⊥平面ABC,
∴BC⊥平面ACD,∴AD⊥BC.
又AD⊥CD,BC∩CD=C,∴AD⊥平面BCD.
(2)由(1)得AD⊥BD,
∴S△ADB=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
∵三棱锥BACD的高BC=2![]() ,
,
S△ACD=![]() ×2×2=2,
×2×2=2,
∴![]() ×2
×2![]() h=
h=![]() ×2×2
×2×2![]() ,解得h=
,解得h=![]() .
.
∴三棱锥CABD的高为![]() .
.
点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】设![]() 是由
是由![]() 个实数组成的
个实数组成的![]() 行
行![]() 列的数表,满足:每个数的绝对值不大于
列的数表,满足:每个数的绝对值不大于![]() ,且所有数的和为零,记
,且所有数的和为零,记![]() 为所有这样的数表组成的集合,对于
为所有这样的数表组成的集合,对于![]() ,记
,记![]() 为
为![]() 的第
的第![]() 行各数之和(
行各数之和(![]() 剟
剟![]()
![]() ),
),![]() 为
为![]() 的第
的第![]() 列各数之和(
列各数之和(![]() 剟
剟![]() ),记
),记![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 中的最小值.
中的最小值.
(![]() )对如下数表
)对如下数表![]() ,求
,求![]() 的值.
的值.
|
|
|
|
|
|
(![]() )设数表
)设数表![]() 形如:
形如:
|
|
|
|
|
|
求![]() 的最大值.
的最大值.
(![]() )给定正整数
)给定正整数![]() ,对于所有的
,对于所有的![]() ,求
,求![]() 的最大值.
的最大值.