题目内容
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示.
)的部分图象如图所示.

(1)求f(x)的最小正周期及解析式.
(2)设g(x)=f(x)-cos2x,求函数g(x)在区间[0, ]上的最大值和最小值.
]上的最大值和最小值.
 )的部分图象如图所示.
)的部分图象如图所示.
(1)求f(x)的最小正周期及解析式.
(2)设g(x)=f(x)-cos2x,求函数g(x)在区间[0,
 ]上的最大值和最小值.
]上的最大值和最小值.(1) f(x)=sin(2x+ )
)
(2) 当2x- =
=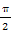 ,即x=
,即x=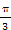 时,g(x)取最大值为1;
时,g(x)取最大值为1;
当2x- =-
=- ,即x=0时,g(x)取最小值为-
,即x=0时,g(x)取最小值为- .
.
 )
)(2) 当2x-
 =
=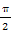 ,即x=
,即x=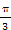 时,g(x)取最大值为1;
时,g(x)取最大值为1;当2x-
 =-
=- ,即x=0时,g(x)取最小值为-
,即x=0时,g(x)取最小值为- .
.【思路点拨】(1)由图象及题设中的限制条件可求A,ω,φ.
(2)将f(x)代入g(x)整理化简为一个三角函数,再由x的范围求最值即可.
解:(1)由图可得A=1, =
=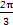 -
- =
=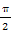 ,所以T=π,所以ω=2.
,所以T=π,所以ω=2.
当x= 时,f(x)=1,
时,f(x)=1,
可得sin(2× +φ)=1,
+φ)=1,
因为|φ|<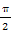 ,所以φ=
,所以φ= .
.
所以f(x)的解析式为f(x)=sin(2x+ ).
).
(2)g(x)=f(x)-cos2x
=sin(2x+ )-cos2x
)-cos2x
=sin2xcos +cos2xsin
+cos2xsin -cos2x
-cos2x
=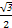 sin2x-
sin2x- cos2x
cos2x
=sin(2x- ).
).
因为0≤x≤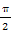 ,所以-
,所以- ≤2x-
≤2x- ≤
≤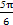 .
.
当2x- =
=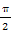 ,即x=
,即x=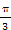 时,g(x)取最大值为1;
时,g(x)取最大值为1;
当2x- =-
=- ,即x=0时,g(x)取最小值为-
,即x=0时,g(x)取最小值为- .
.
【方法技巧】由图象求解析式和性质的方法和技巧
(1)给出图象求y=Asin(ωx+φ)+b的解析式的难点在于ω,φ的确定,本质为待定系数,基本方法是①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到,通常可由平衡点或最值点确定周期T,进而确定ω.
(2)由图象求性质的时候,首先确定解析式,再根据解析式求其性质,要紧扣基本三角函数的性质.例如,单调性、奇偶性、周期性和对称性等都是考查的重点和热点.
(2)将f(x)代入g(x)整理化简为一个三角函数,再由x的范围求最值即可.
解:(1)由图可得A=1,
 =
=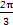 -
- =
=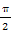 ,所以T=π,所以ω=2.
,所以T=π,所以ω=2.当x=
 时,f(x)=1,
时,f(x)=1,可得sin(2×
 +φ)=1,
+φ)=1,因为|φ|<
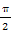 ,所以φ=
,所以φ= .
.所以f(x)的解析式为f(x)=sin(2x+
 ).
).(2)g(x)=f(x)-cos2x
=sin(2x+
 )-cos2x
)-cos2x=sin2xcos
 +cos2xsin
+cos2xsin -cos2x
-cos2x=
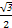 sin2x-
sin2x- cos2x
cos2x=sin(2x-
 ).
).因为0≤x≤
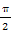 ,所以-
,所以- ≤2x-
≤2x- ≤
≤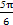 .
.当2x-
 =
=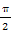 ,即x=
,即x=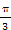 时,g(x)取最大值为1;
时,g(x)取最大值为1;当2x-
 =-
=- ,即x=0时,g(x)取最小值为-
,即x=0时,g(x)取最小值为- .
.【方法技巧】由图象求解析式和性质的方法和技巧
(1)给出图象求y=Asin(ωx+φ)+b的解析式的难点在于ω,φ的确定,本质为待定系数,基本方法是①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到,通常可由平衡点或最值点确定周期T,进而确定ω.
(2)由图象求性质的时候,首先确定解析式,再根据解析式求其性质,要紧扣基本三角函数的性质.例如,单调性、奇偶性、周期性和对称性等都是考查的重点和热点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 -cos2x·cos
-cos2x·cos 在
在 上的单调递增区间为_________.
上的单调递增区间为_________.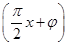 (φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=________.
(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=________.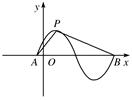
 -φ)-sin(
-φ)-sin( ,0)对称,且在区间[0,
,0)对称,且在区间[0, sin2x+
sin2x+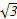 cos2x-
cos2x-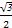 的最小正周期等于( )
的最小正周期等于( )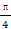
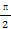
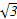 sin(2x+
sin(2x+ ),其中x∈R,则下列结论中正确的是( )
),其中x∈R,则下列结论中正确的是( ) 个单位得到函数f(x)的图象
个单位得到函数f(x)的图象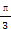 )的图象关于点P(x0,0)对称,若x0∈[-
)的图象关于点P(x0,0)对称,若x0∈[-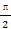 ,0],则x0等于( )
,0],则x0等于( )

 )的部分图像,其中A,B两点之间的距离为5,那么f(-1)=________.
)的部分图像,其中A,B两点之间的距离为5,那么f(-1)=________.
 =________.
=________.