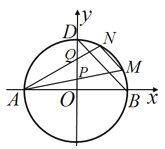题目内容
【题目】已知圆C1:x2+y2-2mx-4my+5m2-4=0(m∈R),圆C2:x2+y2=1.
(1)过定点M(1,-2)作圆C2的切线,求切线的方程;
(2)若圆C1与圆C2相交,求m的取值范围;
(3)已知点P(2,0),圆C1上一点A,圆C2上一点B,求|![]() |的最小值的取值范围.
|的最小值的取值范围.
【答案】(1)x=1或3x+4y+5=0;(2)![]() <m<
<m<![]() ;(3)[
;(3)[![]() ,+∞)
,+∞)
【解析】
(1)当切线斜率不存在时,切线方程为x=1;当切线斜率存在时,设切线方程为y+2=k(x﹣1),由圆心到直线的距离等于半径求得k,则切线方程可求;
(2)由圆C1求得C1(m,2m),r1=2,再求得C2(0,0),r2=1,由圆C1与圆C2相交,得r1﹣r2<|C1C2|<r1+r2,由此可得实数m的范围;
(3)由题意![]() (﹣2,0)+(m﹣2,2m)
(﹣2,0)+(m﹣2,2m)![]() ,求得
,求得![]() 与
与![]() 共线时
共线时![]() 的范围为[1,3],而
的范围为[1,3],而![]() ,其最小值为
,其最小值为![]() ,由此可得当向量
,由此可得当向量![]() 与
与![]() 共线同向且
共线同向且![]() 与
与![]() 反向时,|
反向时,|![]() |的最小值最小,答案可求.
|的最小值最小,答案可求.
(1)当切线斜率不存在时,切线方程为x=1;
当切线斜率存在时,设切线方程为y+2=k(x-1),即kx-y-k-2=0.
由![]() ,解得k=-
,解得k=-![]() ,此时切线方程为3x+4y+5=0.
,此时切线方程为3x+4y+5=0.
∴切线方程为x=1或3x+4y+5=0;
(2)由圆C1:x2+y2-2mx-4my+5m2-4=0,得(x-m)2+(y-2m)2=4,
则C1(m,2m),r1=2,C2(0,0),r2=1.
由圆C1与圆C2相交,得r1-r2<|C1C2|<r1+r2,
∴1![]() ,即
,即![]() <m<
<m<![]() ;
;
(3)如图,O(0,0),C1(m,2m),P(2,0),
则![]() =
=![]() =(-2,0)+(m-2,2m)+
=(-2,0)+(m-2,2m)+![]()
=(m-4,2m)+![]() ,
,
∵![]() 与
与![]() 共线,∴
共线,∴![]() 的范围为[1,3],
的范围为[1,3],
而![]() =
=![]() ,
,
其最小值为![]() ,
,
∴当向量![]() 与
与![]() 共线同向且
共线同向且![]() 与
与![]() 反向时,|
反向时,|![]() |的最小值最小,为
|的最小值最小,为![]() ,
,
∴|![]() |的最小值的取值范围是[
|的最小值的取值范围是[![]() ,+∞).
,+∞).