题目内容
(本小题满分l2分)
如图,在多面体ABCDEF中,ABCD为菱形,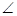 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.
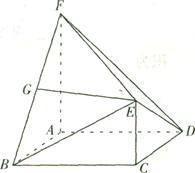
(1)求证:EG 面ABF;
面ABF;
(2)若AF=AB,求二面角B—EF—D的余弦值.
如图,在多面体ABCDEF中,ABCD为菱形,
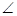 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.
(1)求证:EG
 面ABF;
面ABF;(2)若AF=AB,求二面角B—EF—D的余弦值.
(1)∵在正三角形ABC中,CM AB,又AF
AB,又AF CM∴EG
CM∴EG AB, EG
AB, EG AF,∴EG
AF,∴EG 面ABF.
面ABF.
(2)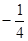
 AB,又AF
AB,又AF CM∴EG
CM∴EG AB, EG
AB, EG AF,∴EG
AF,∴EG 面ABF.
面ABF.(2)
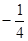
试题分析:(1)取AB的中点M,连结GM,MC,G为BF的中点,
所以GM //FA,又EC
 面ABCD, FA
面ABCD, FA 面ABCD,
面ABCD,∵CE//AF,
∴CE//GM,
∵面CEGM
 面ABCD=CM,
面ABCD=CM,EG// 面ABCD,
∴EG//CM,
∵在正三角形ABC中,CM
 AB,又AF
AB,又AF CM
CM∴EG
 AB, EG
AB, EG AF,
AF,∴EG
 面ABF.
面ABF.(2)建立如图所示的坐标系,设AB=2,
则B(
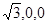 )E(0,1,1) F(0,-1,2)
)E(0,1,1) F(0,-1,2)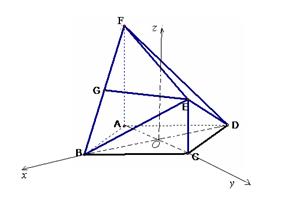
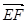 =(0,-2,1) ,
=(0,-2,1) , 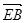 =(
=(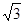 ,-1,-1),
,-1,-1), 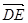 =(
=(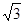 ,1, 1),
,1, 1),设平面BEF的法向量
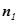 =(
=(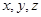 )则
)则 令
令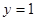 ,则
,则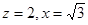 ,
,∴
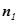 =(
=(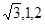 )
) 同理,可求平面DEF的法向量
 =(-
=(-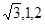 )
)设所求二面角的平面角为
 ,则
,则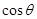 =
=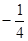 .
.点评:本题考查线面垂直,考查面面角,正确运用线面垂直的判定,求出平面的法向量是解题的关键.

练习册系列答案
相关题目
 ( )
( )



 中,
中, 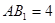 ,底面ABC是正三角形,
,底面ABC是正三角形,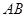 =2.四边形
=2.四边形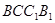 是矩形,二面角
是矩形,二面角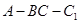 为直二面角,D为
为直二面角,D为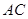 中点。
中点。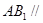 平面
平面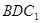 ;
;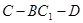 的余弦值.
的余弦值. ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
,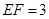 ,
, ,
,  是
是 的中点.
的中点.
 平面
平面 ;
; ;
;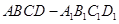 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,若
上,若 平面
平面 ,则
,则 ________.
________.

 中,E为AC中点
中,E为AC中点

 ,
,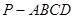 中,四边形
中,四边形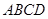 为正方形,
为正方形,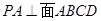 ,且
,且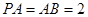 ,
,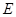 为
为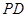 中点.
中点.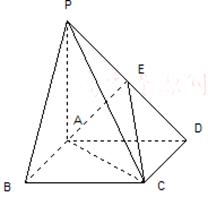
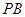 //平面
//平面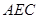 ;
;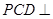 平面
平面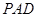 ;
;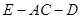 的正弦值.
的正弦值.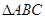 的中心,则直线EF与平面ABC所成的角的正切值是 。
的中心,则直线EF与平面ABC所成的角的正切值是 。