题目内容
如图,在四棱锥P-ABCD中,底面为直角梯形ABCD,AD∥BC,∠BAD=90O,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.(1)求证:PB⊥DM;(2)求CD与平面ADMN所成角的正弦值;(3)在棱PD上是否存在点E,且PE∶ED=λ,使得二面角C-AN-E的平面角为60o.若存在求出λ值,若不存在,请说明理由。

(1)建系,利用 ,证明PB⊥DM
,证明PB⊥DM
(2)
(3)先假设存在,求出法向量,可以算出无解,所以不存在符合要求的解.
 ,证明PB⊥DM
,证明PB⊥DM(2)

(3)先假设存在,求出法向量,可以算出无解,所以不存在符合要求的解.
试题分析:(1)如图以A为原点建立空间直角坐标系

A(0,0,0),B(2,0,0),
C(2,1,0),D(0,2,0)
M(1,
 ,1),N(1,0,1),
,1),N(1,0,1),E(0,m,2-m),P(0,0,2)
 (2,0,-2),
(2,0,-2), (1,-
(1,- ,1),
,1),  ="0"
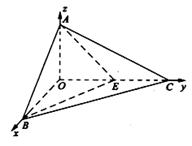
="0" 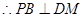
(2)
 =(-2,1,0)平面ADMN法向量
=(-2,1,0)平面ADMN法向量 =(x,y,z),
=(x,y,z), =(0,2,0),
=(0,2,0), =(1,0,1) ,
=(1,0,1) ,所以
 ,即
,即 ,解得
,解得 =(1,0,-1),
=(1,0,-1),设CD与平面ADMN所成角α,则
 .
.(3)设平面ACN法向量
 =(x,y,z),
=(x,y,z),所以
 ,解得
,解得 =(1,-2,-1),
=(1,-2,-1),设
 ,所以
,所以 ,
,同理可以求出平面AEN的法向量
 ,
,因为
 ,所以
,所以 ,
,所以
 ,
,此方程无解,所以不存在符合要求的点.
点评:解决立体几何问题,可以建立空间向量,但是证明时也要根据相应的判定定理和性质定理,定理中要求的条件要一一列举出来,另外还要注意各种角的取值范围.

练习册系列答案
相关题目
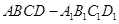 是棱长为1的正方体,四棱锥
是棱长为1的正方体,四棱锥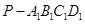 中,
中,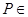 平面
平面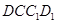 ,
,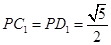 。
。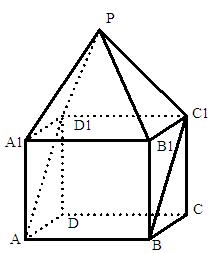
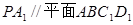
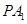 与平面
与平面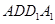 所成角的正切值。
所成角的正切值。
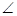 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA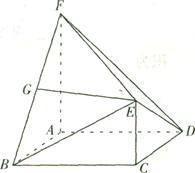
 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,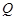 是棱
是棱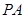 上的动点.
上的动点.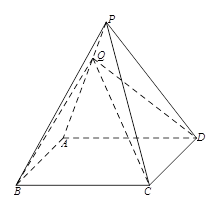
 是
是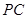 //平面
//平面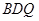 ;
;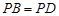 ,求证:
,求证: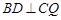 ;
;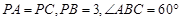 ,求四棱锥
,求四棱锥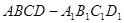 中,下列结论错误的是
中,下列结论错误的是 ∥平面
∥平面
 平面
平面

 与
与 所成的角是45º
所成的角是45º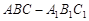 中,
中,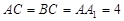 ,
, 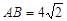 ,若
,若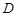 是
是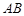 中点.
中点.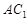 ∥平面
∥平面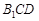 ;
; 所成的角.
所成的角.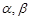 是两个不重合的平面,则下列命题中不正确的一个是
是两个不重合的平面,则下列命题中不正确的一个是 则
则 ∥
∥
 ,则
,则 ∥
∥
 则
则
 ,则
,则