题目内容
若非零函数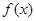 对任意实数
对任意实数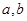 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当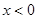 时,
时,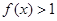 .
.
(1)求证: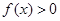 ;
;
(2)求证: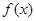 为减函数;
为减函数;
(3)当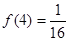 时,解不等式
时,解不等式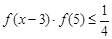
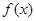 对任意实数
对任意实数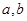 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当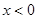 时,
时,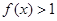 .
.(1)求证:
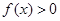 ;
; (2)求证:
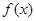 为减函数;
为减函数;(3)当
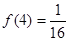 时,解不等式
时,解不等式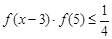
(1)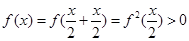 (2)设
(2)设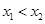 则
则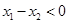
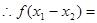
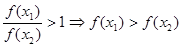 ,
,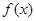 为减函数
为减函数
(3)由 原不等式转化为
原不等式转化为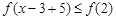 ,
,
结合(2)得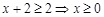
故不等式的解集为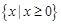 .
.
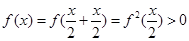 (2)设
(2)设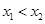 则
则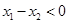
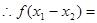
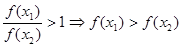 ,
,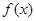 为减函数
为减函数(3)由
 原不等式转化为
原不等式转化为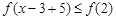 ,
,结合(2)得
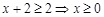
故不等式的解集为
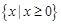 .
.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 时,画出函数
时,画出函数 的一个大致的图象,并指出函数的单调递增区间;
的一个大致的图象,并指出函数的单调递增区间; 在区间
在区间 内有零点,求实数
内有零点,求实数 的取值范围.
的取值范围. 满足
满足 单调递增,如果
单调递增,如果 的值( )
的值( ) 在
在 上为增函数,且f(
上为增函数,且f( )=
)= ,f(1)=2,集合
,f(1)=2,集合 ,关于
,关于 的不等式
的不等式 的解集为
的解集为 ,求使
,求使 的实数
的实数 的取值范围.
的取值范围.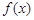 是定义在R上的函数,且对任意
是定义在R上的函数,且对任意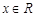 ,满足
,满足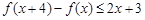 ,
,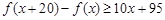 ,且
,且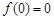 ,则
,则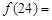 ______
______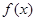 在
在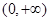 上是增函数,试问
上是增函数,试问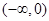 上是增函数还是减函数?请证明你的结论。
上是增函数还是减函数?请证明你的结论。 时f(x)是增函数,则
时f(x)是增函数,则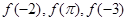 的大小关系是( )
的大小关系是( )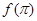 >
>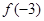 >
>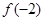
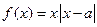 ,若对于任意
,若对于任意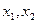
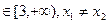 ,不等式
,不等式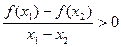 恒成立,则实数
恒成立,则实数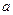 的取值范围是
的取值范围是