题目内容
定义在R上的函数 满足
满足 单调递增,如果
单调递增,如果 的值( )
的值( )
 满足
满足 单调递增,如果
单调递增,如果 的值( )
的值( )| A.恒小于0 | B.恒大于零 | C.可能为零 | D.非负数 |
A
因为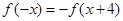 ,所以
,所以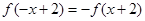 ,则函数
,则函数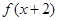 是定义在R上的奇函数,从而可得函数
是定义在R上的奇函数,从而可得函数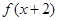 的图象关于原点对称,所以函数
的图象关于原点对称,所以函数 的图象关于点
的图象关于点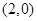 对称。因为当
对称。因为当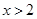 时
时 单调递增,所以当
单调递增,所以当 时
时 也单调递增,且
也单调递增,且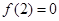 。因为
。因为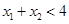 ,所以
,所以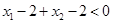 ,而
,而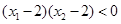 ,且不妨设
,且不妨设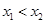 ,所以
,所以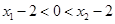 即
即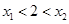 且
且 。所以由函数对称性可知,
。所以由函数对称性可知,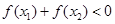 ,故选A
,故选A
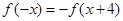 ,所以
,所以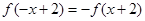 ,则函数
,则函数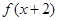 是定义在R上的奇函数,从而可得函数
是定义在R上的奇函数,从而可得函数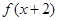 的图象关于原点对称,所以函数
的图象关于原点对称,所以函数 的图象关于点
的图象关于点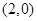 对称。因为当
对称。因为当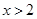 时
时 单调递增,所以当
单调递增,所以当 时
时 也单调递增,且
也单调递增,且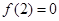 。因为
。因为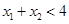 ,所以
,所以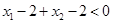 ,而
,而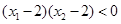 ,且不妨设
,且不妨设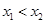 ,所以
,所以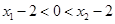 即
即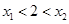 且
且 。所以由函数对称性可知,
。所以由函数对称性可知,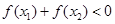 ,故选A
,故选A
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
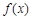 的定义域为
的定义域为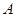 ,若
,若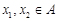 且
且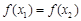 时总有
时总有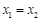 ,则称
,则称
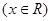 是单函数。下列命题:
是单函数。下列命题: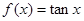
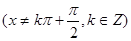 是单函数;
是单函数;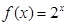
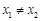 ,则
,则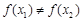 ;
;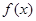 是定义在
是定义在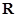 上的增函数,且对于任意的
上的增函数,且对于任意的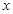 都有
都有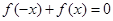 恒成立. 如果实数
恒成立. 如果实数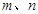 满足不等式
满足不等式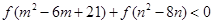 ,那么
,那么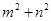 的取值范围是
的取值范围是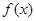 对任意实数
对任意实数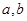 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当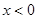 时,
时,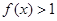 .
.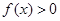 ;
; 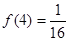 时,解不等式
时,解不等式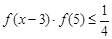
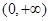 的是( )
的是( )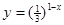 B.
B. 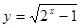 C.
C. 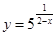 D
D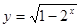
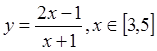 的最小值和最大值。
的最小值和最大值。 在
在 上为减函数,则
上为减函数,则 的取值范围为 。
的取值范围为 。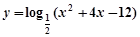 的单调递增区间是
的单调递增区间是