题目内容
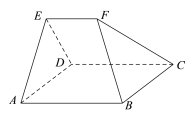
【题目】如图,在五面体![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,平面
的正方形,平面![]() ⊥平面
⊥平面![]() ,
, ![]() .
.
(Ⅰ) 求证:![]() ;
;
(Ⅱ) 求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅲ) 在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ⊥平面
⊥平面![]() ? 说明理由.
? 说明理由.
【答案】(Ⅰ)详见解析(Ⅱ)详见解析(Ⅲ)存在点N符合题意
【解析】
(Ⅰ) 推导出AB∥CD.由此能证明CD∥平面ABFE.(Ⅱ) 推导出AE⊥DE,AB⊥AD,从而AB⊥平面ADE,进而 AB⊥DE,由此能证明DE⊥平面ABFE,从而平面ABFE⊥平面CDEF.(Ⅲ)取CD的中点N,连接FN,推导出四边形EDNF是平行四边形,从而FN∥DE,由DE⊥平面ABFE,能证明FN⊥平面ABFE.
证明:(Ⅰ)在五面体![]() 中,因为四边形
中,因为四边形![]() 是正方形,
是正方形,
所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)因为![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
因为四边形![]() 是正方形,所以
是正方形,所以![]() .
.
因为平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,
![]()
所以![]() ⊥平面
⊥平面![]() .
.
因为![]() ,所以
,所以![]() ⊥
⊥![]() .
.
因为![]() 所以
所以![]() ⊥平面
⊥平面![]()
因为![]() ,所以平面
,所以平面![]() ⊥平面
⊥平面![]() .
.
(Ⅲ)在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ⊥平面
⊥平面![]() .
.
证明如下:
取![]() 的中点
的中点![]() ,连接
,连接![]() .
.

由(Ⅰ)知,![]() ,
,
![]() ,
,
所以![]() .
.
因为![]()
所以![]() .
.
所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .
.
由(Ⅱ)知,![]() ⊥平面
⊥平面![]() ,
,
所以![]() .
.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: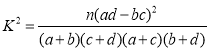 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%