题目内容
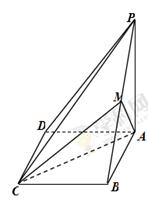
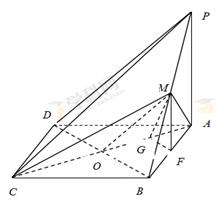
如图,在四棱锥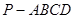 中,
中,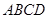 为平行四边形,且
为平行四边形,且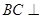 平面
平面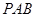 ,
,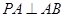 ,
,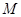 为
为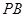 的中点,
的中点,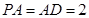 .
.
(Ⅰ) 求证: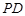 //
//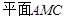 ;
;
(Ⅱ)若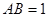 , 求二面角
, 求二面角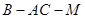 的余弦值.
的余弦值.
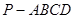 中,
中,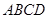 为平行四边形,且
为平行四边形,且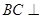 平面
平面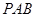 ,
,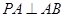 ,
,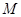 为
为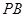 的中点,
的中点,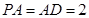 .
.
(Ⅰ) 求证:
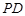 //
//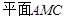 ;
;(Ⅱ)若
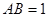 , 求二面角
, 求二面角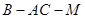 的余弦值.
的余弦值.(Ⅰ)详见解析;(Ⅱ)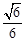 .
.
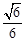 .
.试题分析:(Ⅰ)依题意,设
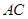 与
与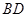 的交点
的交点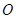 ,说明
,说明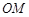 为
为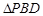 的中位线,
的中位线,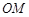 //
//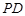 ,从而
,从而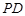 //
//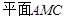 ;(Ⅱ) 用定义法与向量法求解,用定义法,必须作出二面角的平面角,在利用相似三角形对应边成比例及直角三角形中三角函数的定义求解;用向量法,需要建立恰当的空间直角坐标系,本题以点
;(Ⅱ) 用定义法与向量法求解,用定义法,必须作出二面角的平面角,在利用相似三角形对应边成比例及直角三角形中三角函数的定义求解;用向量法,需要建立恰当的空间直角坐标系,本题以点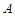 为坐标原点,分别以
为坐标原点,分别以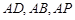 所在直线为
所在直线为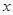 轴,
轴,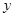 轴和
轴和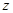 轴,建立空间直角坐标系
轴,建立空间直角坐标系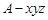 最佳,求平面
最佳,求平面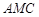 的法向量
的法向量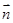 与平面
与平面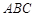 的一个法向量为
的一个法向量为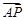 , 利用公式
, 利用公式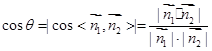 求解.
求解.试题解析:(Ⅰ)证明: 连接
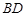 ,设
,设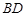 与
与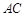 相交于点
相交于点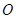 ,连接
,连接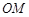 ,
,
∵ 四边形
 是平行四边形,∴点
是平行四边形,∴点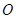 为
为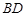 的中点.
的中点.∵
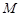 为
为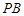 的中点,∴
的中点,∴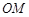 为
为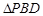 的中位线,
的中位线,∴
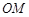 //
//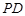 , 2分
, 2分∵
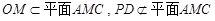 ,
,∴
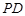 //
//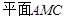 . 4分
. 4分(Ⅱ) 解法一 : ∵
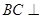 平面
平面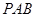 ,
,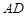 //
// , 则
, 则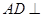 平面
平面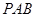 ,故
,故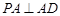 ,
,又
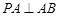 , 且
, 且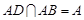 ,
,∴
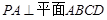 . 6分
. 6分取
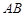 的中点
的中点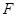 ,连接
,连接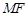 ,则
,则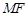 //
//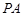 ,且
,且 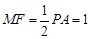 .
. ∴
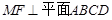 .
.作
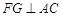 ,垂足为
,垂足为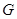 ,连接
,连接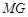 ,由于
,由于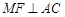 ,且
,且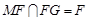 ,
,∴
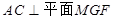 ,∴
,∴ 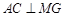 .
.∴
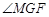 为二面角
为二面角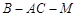 的平面角. 9分
的平面角. 9分由
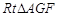 ∽
∽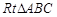 ,得
,得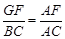 ,得
,得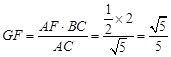 ,
,在
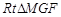 中,
中,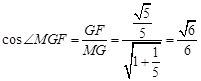 .
.∴ 二面角
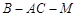 的余弦值为
的余弦值为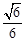 . 12分
. 12分(Ⅱ) 解法二: ∵
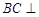 平面
平面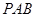 ,
,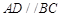 , 则
, 则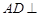 平面
平面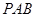 ,故
,故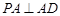 ,
,又
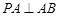 , 且
, 且 ,∴
,∴ . 6分
. 6分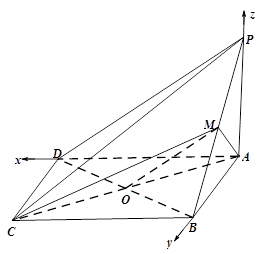
以点
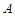 为坐标原点,分别以
为坐标原点,分别以 所在直线为
所在直线为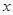 轴,
轴,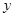 轴和
轴和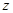 轴,建立空间直角坐标系
轴,建立空间直角坐标系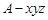 .则
.则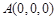 ,
,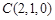 ,
,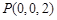 ,
,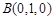 ,
,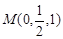 ,
, ∴
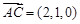 ,
, 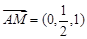 ,
,求得平面
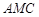 的法向量为
的法向量为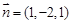 ,
, 又平面
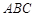 的一个法向量为
的一个法向量为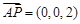 ,
, ∴
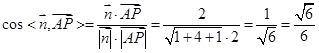 .
. ∴ 二面角
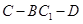 的余弦值为
的余弦值为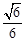 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
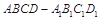 ,中,
,中,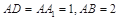 ,点
,点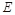 在棱AB上移动.
在棱AB上移动.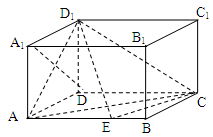
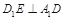 ;
; 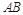 的中点时,求点
的中点时,求点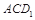 的距离;
的距离; 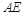 等于何值时,二面角
等于何值时,二面角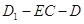 的大小为
的大小为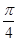 .
.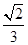 a,则MN与平面BB1C1C的位置关系是________.
a,则MN与平面BB1C1C的位置关系是________.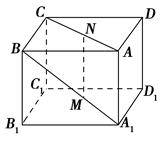
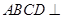 平面
平面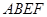 ,四边形
,四边形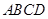 是正方形,四边形
是正方形,四边形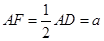 ,
,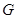 是
是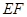 的中点,则
的中点,则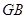 与平面
与平面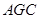 所成角的正弦值为( )
所成角的正弦值为( )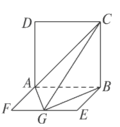
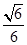
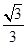
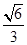
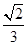
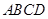 -
-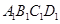 中,
中,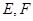 分别为
分别为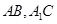 的中点. 应用空间向量方法求解下列问题.
的中点. 应用空间向量方法求解下列问题. 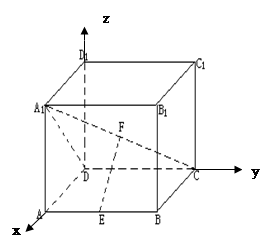
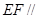 平面
平面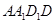 ;
;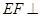 平面
平面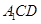 .
. ,使得平面
,使得平面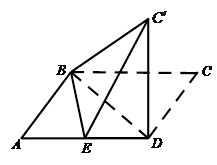
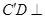 平面ABD;
平面ABD;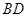 与平面
与平面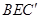 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.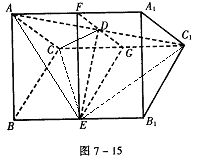
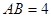
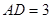
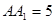 则 .
则 .